题目内容
已知椭圆E的长轴的一个端点是抛物线
(I)求椭圆E的方程;
(II)过点C(-1,0),斜率为k的动直线与椭圆E相交于A、B两点,请问x轴上是否存在点M,使 恒为常数?若存在,求出点M的坐标;若不存在,请说明理由.
恒为常数?若存在,求出点M的坐标;若不存在,请说明理由.
解:(I)由题意,椭圆的焦点在x轴上,且a= ,c=e•a=
,c=e•a= ×
× =
= ,故b=
,故b=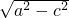 =
= =
= ,
,
所以,椭圆E的方程为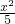 +
+ =1,即x2+3y2=5.
=1,即x2+3y2=5.
(II)假设存在点M符合题意,设AB:y=k(x+1),
代入方程E:x2+3y2=5,得(3k2+1)x2+6k2x+3k2-5=0;
设A(x1,y1),B(x2,y2),M(m,0),则
x1+x2=- ,x1x2=
,x1x2= ;
;
∴ •
• =(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2=m2+2m-
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2=m2+2m- -
- ,
,
要使上式与k无关,则有6m+14=0,解得m=- ;
;
所以,存在点M(- ,0)满足题意.
,0)满足题意.
分析:(I)椭圆的焦点在x轴上,且a= ,e=
,e= ,故c、b可求,所以椭圆E的方程可以写出来.
,故c、b可求,所以椭圆E的方程可以写出来.
(II)假设存在点M符合题意,设AB为y=k(x+1),代入方程E可得关于x的一元二次方程(*);
设A(x1,y1),B(x2,y2),M(m,0),由方程(*)根与系数的关系可得,x1+x2,x1x2;计算 •
• 得关于m、k的代数式,要使这个代数式与k无关,可以得到m的值;从而得点M.
得关于m、k的代数式,要使这个代数式与k无关,可以得到m的值;从而得点M.
点评:本题考查了直线与圆锥曲线的综合应用问题,也考查了椭圆的标准方程及其几何性质,考查了一定的计算能力.
 ,c=e•a=
,c=e•a= ×
× =
= ,故b=
,故b=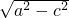 =
= =
= ,
,所以,椭圆E的方程为
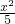 +
+ =1,即x2+3y2=5.
=1,即x2+3y2=5.(II)假设存在点M符合题意,设AB:y=k(x+1),
代入方程E:x2+3y2=5,得(3k2+1)x2+6k2x+3k2-5=0;
设A(x1,y1),B(x2,y2),M(m,0),则
x1+x2=-
 ,x1x2=
,x1x2= ;
;∴
 •
• =(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2=m2+2m-
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2=m2+2m- -
- ,
,要使上式与k无关,则有6m+14=0,解得m=-
 ;
;所以,存在点M(-
 ,0)满足题意.
,0)满足题意.分析:(I)椭圆的焦点在x轴上,且a=
 ,e=
,e= ,故c、b可求,所以椭圆E的方程可以写出来.
,故c、b可求,所以椭圆E的方程可以写出来.(II)假设存在点M符合题意,设AB为y=k(x+1),代入方程E可得关于x的一元二次方程(*);
设A(x1,y1),B(x2,y2),M(m,0),由方程(*)根与系数的关系可得,x1+x2,x1x2;计算
 •
• 得关于m、k的代数式,要使这个代数式与k无关,可以得到m的值;从而得点M.
得关于m、k的代数式,要使这个代数式与k无关,可以得到m的值;从而得点M.点评:本题考查了直线与圆锥曲线的综合应用问题,也考查了椭圆的标准方程及其几何性质,考查了一定的计算能力.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目