题目内容
（2012•顺河区一模）已知椭圆E的短轴长为6，焦点F到长轴端点的距离为9，则椭圆E的离心率等于
．
| 4 |
| 5 |
| 4 |
| 5 |
分析：依题意，可求得椭圆E的短半轴长b=3，a±c=9，利用椭圆的简单性质即可求得椭圆E的离心率．
解答：解：设椭圆E的短轴长为2b，长轴长为2a，焦距为2c，
则2b=6，即b=3；a+c=9或a-c=9．
若a+c=9，①
∵b2=a2-c2=（a+c）（a-c）=9（a-c）=32=9，
∴a-c=1②
由①②得：a=4，c=4，
∴椭圆E的离心率e=
；
若a-c=9，③
则a+c=1，即得a=5，c=-4，这不可能．
故椭圆E的离心率为
．
故答案为：
．
则2b=6，即b=3；a+c=9或a-c=9．
若a+c=9，①
∵b2=a2-c2=（a+c）（a-c）=9（a-c）=32=9，
∴a-c=1②
由①②得：a=4，c=4，
∴椭圆E的离心率e=
| 4 |
| 5 |
若a-c=9，③
则a+c=1，即得a=5，c=-4，这不可能．
故椭圆E的离心率为
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题考查椭圆的简单性质，考查分类讨论思想与方程思想的综合运用，属于中档题．
练习册系列答案
相关题目
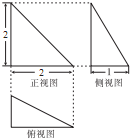（2012•顺河区一模）三棱椎A-BCD的三视图为如图所示的三个直角三角形，则三棱锥A-BCD的表面积为（ ）
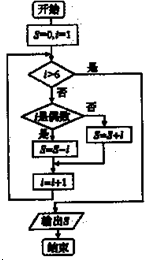（2012•顺河区一模）执行如图所给的程序框图，则运行后输出的结果是（ ）