题目内容
复数z1= +(10-a2)i,z2=
+(10-a2)i,z2= +(2a-5)i,若
+(2a-5)i,若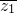 +z2是实数,求实数a的值.
+z2是实数,求实数a的值.
解:∵z1= +(10-a2)i,z2=
+(10-a2)i,z2= +(2a-5)i,
+(2a-5)i,
∴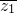 +z2是=[
+z2是=[ +(a2-10)i]+[
+(a2-10)i]+[ +(2a-5)i]
+(2a-5)i]
=( +
+ )+(a2-10+2a-5)i
)+(a2-10+2a-5)i
= +(a2+2a-15)i,
+(a2+2a-15)i,
∵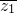 +z2是实数,
+z2是实数,
∴a2+2a-15=0,解得a=-5或a=3.
又分母a+5≠0,
∴a≠-5,
故a=3.
分析:可求得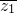 +z2=
+z2= +(a2+2a-15)i,利用其虚部为0即可求得实数a的值.
+(a2+2a-15)i,利用其虚部为0即可求得实数a的值.
点评:本题考查复数的基本概念,考查转化思想与方程思想,属于中档题.
 +(10-a2)i,z2=
+(10-a2)i,z2= +(2a-5)i,
+(2a-5)i,∴
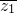 +z2是=[
+z2是=[ +(a2-10)i]+[
+(a2-10)i]+[ +(2a-5)i]
+(2a-5)i]=(
 +
+ )+(a2-10+2a-5)i
)+(a2-10+2a-5)i=
 +(a2+2a-15)i,
+(a2+2a-15)i,∵
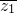 +z2是实数,
+z2是实数,∴a2+2a-15=0,解得a=-5或a=3.
又分母a+5≠0,
∴a≠-5,
故a=3.
分析:可求得
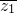 +z2=
+z2= +(a2+2a-15)i,利用其虚部为0即可求得实数a的值.
+(a2+2a-15)i,利用其虚部为0即可求得实数a的值.点评:本题考查复数的基本概念,考查转化思想与方程思想,属于中档题.

练习册系列答案
相关题目