题目内容
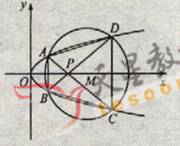(22) （本小题满分12分）（注意：在试题卷上作答无效）如图，已知抛物线
与圆
相交于A、B、C、D四个点。
（Ⅰ）求r的取值范围
（Ⅱ）当四边形ABCD的面积最大时，求对角线AC、BD的交点P的坐标。
（Ⅰ）
（Ⅱ）（
）
解析:
（Ⅰ）联立方程组
与
，可得
，所以方程由两个不等式正根
由此得到
解得
，所以r的范围为
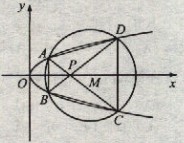
（Ⅱ）不妨设E与M的四个交点坐标分别为设
直线AC,BD的方程分别为
，
解得点p的坐标为
设t=
，由t=
及（1）可知
由于四边形ABCD为等腰梯形，因而其面积
将
代入上式，并令
，得
求导数，
令
，解得
当
时，
，当
，；当
时，
当且仅当时，
由最大值，即四边形ABCD的面积最大，故所求的点P的坐标为（）
练习册系列答案
相关题目
(本小题12分)某次测试有900人参加，满分为100分，为了了解成绩情况，抽取了50名同学的成绩进行统计.
(1) 将频率分布表补充完整； (2) 绘制频率分布直方图；
(3) 估计全体学生中及格(不低于60分)的人数大约是多少.
| 分 组 | 频数 | 频率 |
| [40，50） | 4 | |
| [50，60） | 0.12 | |
| [60，70） | 9 | |
| [70，80） | 15 | |
| [80，90） | 0.22 | |
| [90，100） | ||
| 合 计 | 50 |
 |