题目内容
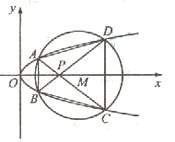
 如图,已知抛物线
如图,已知抛物线![]()
![]() 与圆
与圆![]() 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
(Ⅰ)求r的取值范围
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
解析:(Ⅰ)将抛物线![]() 代入圆
代入圆![]() 的方程,消去
的方程,消去![]() ,整理得
,整理得![]() .............(1)
.............(1)
抛物线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 、
、![]() 、
、![]() 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴ 即
即 。解这个方程组得
。解这个方程组得![]()
![]() .
.
(II) 设四个交点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]() 。
。
则由(I)根据韦达定理有![]() ,
,![]()
则![]()
![]()
令![]() ,则
,则![]() 下面求
下面求![]() 的最大值。
的最大值。
方法1:由三次均值有:
![]()
![]()
当且仅当![]() ,即
,即![]() 时取最大值。经检验此时
时取最大值。经检验此时![]() 满足题意。
满足题意。
法2:设四个交点的坐标分别为![]() 、
、![]() 、
、![]() 、
、![]()
则直线AC、BD的方程分别为

解得点P的坐标为![]() 。
。
设![]() ,由
,由![]() 及(Ⅰ)得
及(Ⅰ)得![]()
![]()
由于四边形ABCD为等腰梯形,因而其面积![]()
则![]() 将
将![]() ,
,![]() 代入上式,并令
代入上式,并令![]() ,等
,等
![]() ,
,
∴![]() ,
,
令![]() 得
得![]() ,或
,或![]() (舍去)
(舍去)
当![]() 时,
时,![]() ;当
;当![]() 时
时![]() ;当
;当![]() 时,
时,![]()
故当且仅当![]() 时,
时,![]() 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为![]() 。
。 ![]()

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
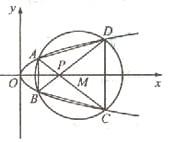 如图,已知抛物线
如图,已知抛物线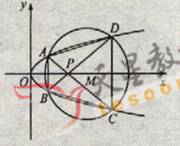 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线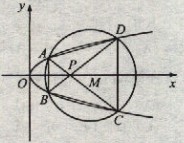
 如图,已知抛物线
如图,已知抛物线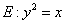
 与圆
与圆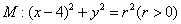 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。