Question

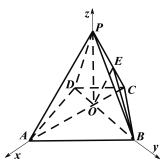
【题目】已知四棱锥的底面是等腰梯形，，，，，.

（Ⅰ）证明：平面平面；

（Ⅱ）点是棱上一点，且平面，求二面角的余弦值.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）.

【解析】

（Ⅰ）首先通过计算得，再利用判定定理转化为线面垂直，从而得到面面垂直；（Ⅱ）首先通过垂直关系的判定正确建立空间直角坐标系找好的坐标，然后将线面平行即平面转化为线线平行，从而确定平面的法向量，最后根据法向量求出二面角的余弦.

（Ⅰ）证明：等腰梯形中，∽，

所以，又，所以，所以.

所以，所以，即，

又因为，且于点，

所以平面，又因为平面，因此平面平面.

（Ⅱ）连接，由（Ⅰ）知，平面，所以，所以，

所以，即，

如图以所在直线分别为轴，轴，轴建立空间直角坐标系，

则，平面的法向量，

因为平面，平面，

平面平面，所以，

设平面的法向量为，则，即，

，令，则，

所以，所以所求二面角的余弦值是.