题目内容
已知 为椭圆
为椭圆
 的左、右焦点,
的左、右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于
 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
 为椭圆
为椭圆
 的左、右焦点,
的左、右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于
 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过左焦点
 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.(1) (2) 即
(2) 即 或
或
 (2) 即
(2) 即 或
或
本试题主要是考查了椭圆的方程以及直线与椭圆的位置关系的运用。
解:(Ⅰ)由条件知 ,且
,且 ,由
,由 ,
,
解得, , ……………………………4分
, ……………………………4分
所以椭圆方程为 . ………………………… 5分
. ………………………… 5分
(Ⅱ)设点A ,B
,B ,
,
当 轴时,A
轴时,A ,B
,B ,所以
,所以 , ………6分
, ………6分
设直线 的方程为
的方程为 ,
,
代入椭圆方程得 . ……………8分
. ……………8分
所以 ……………………… 9分
……………………… 9分
由 ,得
,得 . …………………… 10分
. …………………… 10分
 .
.
代入得 ,
,
解得 . …………………… 12分
. …………………… 12分
所以直线 的方程为
的方程为 .
.
即 或
或 .
.
解:(Ⅰ)由条件知
 ,且
,且 ,由
,由 ,
, 解得,
 , ……………………………4分
, ……………………………4分所以椭圆方程为
 . ………………………… 5分
. ………………………… 5分(Ⅱ)设点A
 ,B
,B ,
, 当
 轴时,A
轴时,A ,B
,B ,所以
,所以 , ………6分
, ………6分设直线
 的方程为
的方程为 ,
, 代入椭圆方程得
 . ……………8分
. ……………8分所以
 ……………………… 9分
……………………… 9分由
 ,得
,得 . …………………… 10分
. …………………… 10分 .
.代入得
 ,
,解得
 . …………………… 12分
. …………………… 12分所以直线
 的方程为
的方程为 .
. 即
 或
或 .
. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
.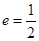 ,过左焦点
,过左焦点 作直线
作直线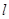 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线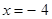 交于点
交于点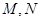 .
.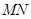 为直径的圆经过焦点
为直径的圆经过焦点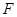 .
. :
: (
( ),直线
),直线 为圆
为圆 :
: 的一条切线并且过椭圆的右焦点,记椭圆的离心率为
的一条切线并且过椭圆的右焦点,记椭圆的离心率为 .
. ,求
,求 的离心率为
的离心率为 ,且过点
,且过点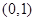 ,过
,过 的右焦点
的右焦点 任作直线
任作直线 ,设
,设 ,
, 两点(异于
两点(异于 ,
, ,记
,记 .
.
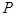 是椭圆
是椭圆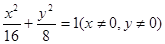 上的动点,
上的动点,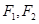 为椭圆的两个焦点,
为椭圆的两个焦点,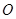 是坐标原点,若
是坐标原点,若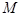 是
是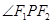 的角平分线上一点,且
的角平分线上一点,且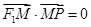 ,则
,则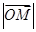 的取值范围是( )
的取值范围是( )
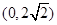
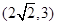
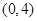
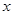 轴上,离心率为
轴上,离心率为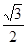 ,它与直线
,它与直线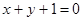 相交于P、Q两点,若
相交于P、Q两点,若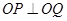 ,求椭圆方程。
,求椭圆方程。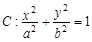 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆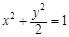 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
 R).
R). ,求曲线
,求曲线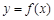 在点
在点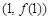 处的的切线方程;
处的的切线方程; 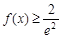 对任意
对任意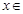
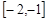 恒成立,求实数
恒成立,求实数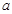 的取值范围.
的取值范围. 上一点,F1、F2是椭圆的两个焦点,
上一点,F1、F2是椭圆的两个焦点, ,则△F1PF2的面积是 .
,则△F1PF2的面积是 .