题目内容
若实数x,y满足
,则
的取值范围为( )
|
| y+1 |
| x+1 |
A、[
| ||||
B、[
| ||||
C、[-
| ||||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由题意实数x,y满足不等式组
,由此不等式组画出可行域,在令目标函数z=
,利用该式子的几何含义表示的为:可行域内任意一点与定点(-1,-1)构成的斜率,进而求解.
|
| y+1 |
| x+1 |
解答:
 解:实数x,y满足不等式组
解:实数x,y满足不等式组
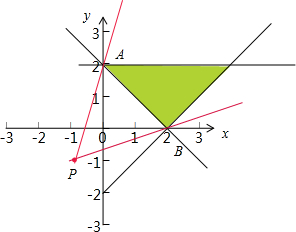
,画出可行域为图示的阴影区域:
由于令目标函数z=
,利用该式子的几何含义表示的为:可行域内任意一点与定点(-1,-1)构成的斜率,画图可知当目标函数过点A(0,2)时构成的可行域内的所有点中斜率最大,最大值为:
=3.
当目标函数过点B(2,0)时构成的可行域内的所有点中斜率最小,最小值为
=
.
实数x,y满足
,则
的取值范围为:[
,3].
故选:A.
 解:实数x,y满足不等式组
解:实数x,y满足不等式组
|
由于令目标函数z=
| y+1 |
| x+1 |
| 2-(-1) |
| 0-(-1) |
当目标函数过点B(2,0)时构成的可行域内的所有点中斜率最小,最小值为
| 0+1 |
| 2+1 |
| 1 |
| 3 |
实数x,y满足
|
| y+1 |
| x+1 |
| 1 |
| 3 |
故选:A.
点评:此题考查了线性规划有不等式组画可行域,还考查了利用目标函数的几何含义求其最值,重点考查了学生的数形结合的能力.

练习册系列答案
相关题目
已知AE是△ABC的中线,若∠A=120°,
•
=-2,则|
|的最小值是( )
| AC |
| AB |
| AE |
| A、-1 | B、0 | C、1 | D、2 |
已知α,β∈(
,π),sin
+cos
=
,sin(α-β)=-
,则cosβ的值为( )
| π |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
 如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.
如图,在直径为1的圆O中,作一关于圆心对称、邻边互相垂直的十字形,其中y>x>0.