题目内容
(本小题满分13分)在平面直角坐标系 中,椭圆
中,椭圆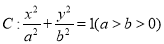 过点
过点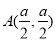 和点
和点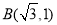 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点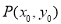 在椭圆
在椭圆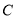 上,
上,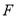 为椭圆的左焦点,直线
为椭圆的左焦点,直线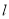 的方程为
的方程为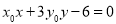 .
.
(i)求证:直线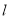 与椭圆
与椭圆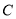 有唯一的公共点;
有唯一的公共点;
(ii)若点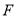 关于直线
关于直线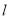 的对称点为
的对称点为 ,探索:当点
,探索:当点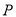 在椭圆
在椭圆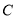 上运动时,直线
上运动时,直线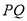 是否过定点?
是否过定点?
若过定点,求出此定点的坐标;若不过定点,请说明理由.
(1)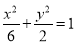 ;(2)(i)详见解析;(ii)定点坐标为
;(2)(i)详见解析;(ii)定点坐标为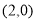 .
.
【解析】
试题分析:(1)根据题意,将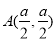 和点
和点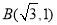 分别代入椭圆方程,即可得到关于
分别代入椭圆方程,即可得到关于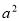 ,
,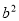 的方程组:
的方程组: ,
, ,从而可以解得
,从而可以解得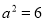 ,
,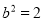 ,即椭圆
,即椭圆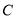 的方程为
的方程为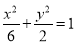 ;(2)(ii)分析题意可知,要证直线
;(2)(ii)分析题意可知,要证直线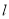 与椭圆
与椭圆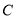 只有一个公共点,等价于将直线方程与椭圆方程联立所得的方程组只有唯一的解,因此考虑将方程联立,化简变形可得
只有一个公共点,等价于将直线方程与椭圆方程联立所得的方程组只有唯一的解,因此考虑将方程联立,化简变形可得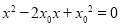 ,易知其
,易知其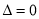 ,从而得证;(ii)由题意可知
,从而得证;(ii)由题意可知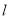 为线段
为线段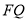 的中垂线,因此利用线段
的中垂线,因此利用线段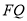 与直线
与直线 垂直以及线段
垂直以及线段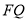 的中点在直线
的中点在直线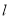 上可求得点
上可求得点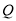 的坐标为
的坐标为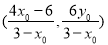 ,以下需分类讨论列出直线
,以下需分类讨论列出直线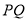 的解析式:当
的解析式:当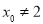 时,直线
时,直线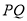 的斜率
的斜率 ,直线
,直线 的方程为
的方程为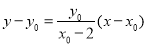 ,即
,即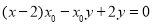 ,直线过定点
,直线过定点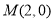 ,当
,当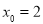 时,
时,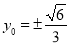 ,此时
,此时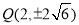 ,直线
,直线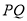 过点
过点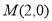 ,即可证明直线
,即可证明直线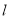 恒过定点
恒过定点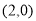 .
.
试题解析:(1)∵ ,且
,且 ,∴
,∴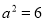 ,
,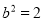 ,∴椭圆
,∴椭圆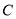 的方程为
的方程为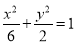 .
.
(2)(i)联立方程组 ,整理为
,整理为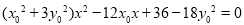 …①,
…①,
∵ 在椭圆
在椭圆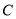 上,∴
上,∴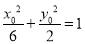 ,即
,即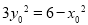 ,∴方程①为
,∴方程①为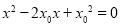 ,即
,即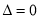 ,∴直线
,∴直线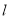 与椭圆
与椭圆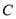 有唯一的公共点; (ii)∵
有唯一的公共点; (ii)∵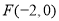 ,∴过点
,∴过点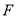 且与
且与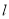 垂直的直线方程为
垂直的直线方程为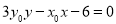 ,
,
∵联立方程组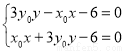 ,∴
,∴ ,∵
,∵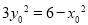 ,且
,且 ,∴
,∴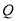 点坐标为
点坐标为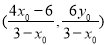 ,当
,当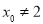 时,直线
时,直线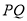 的斜率
的斜率 ,
,
∵直线 的方程为
的方程为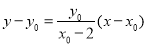 ,即
,即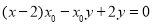 ,∴直线过定点
,∴直线过定点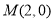 ,
,
当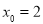 时,
时,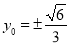 ,此时
,此时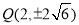 ,直线
,直线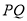 过点
过点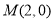 ,综上所述,直线过定点
,综上所述,直线过定点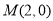 .
.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系;3.直线中的对称问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的一条渐近线与圆
的一条渐近线与圆 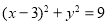 相变于A.B两点,若
相变于A.B两点,若 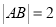 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) C 3 D.4
C 3 D.4 ,则
,则 ___________.
___________. 和平面
和平面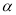 ,则下列命题正确的是( )
,则下列命题正确的是( )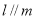 ,
, ,则
,则
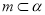 ,则
,则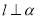 ,
,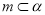 ,则
,则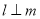
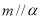
 ,且
,且 ,给出下列命题:
,给出下列命题: ;
; ;
; ;
; 时,
时, .
.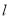 上有无数个点不在平面
上有无数个点不在平面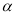 内,则
内,则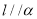 ;
;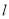 与平面
与平面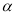 平行,则
平行,则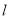 与平面
与平面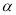 内的任意一条直线都平行;
内的任意一条直线都平行;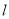 与平面
与平面 B.
B.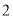 C.
C.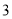 D.
D.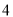
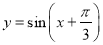 的图象,可将函数
的图象,可将函数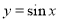 的图象向左平移
的图象向左平移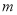 个单位长度,或向右平移
个单位长度,或向右平移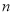 个单位长度(
个单位长度(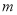 ,
,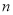 均为正数),则
均为正数),则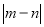 的最小值是( )
的最小值是( )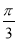 B.
B.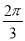 C.
C.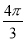 D.
D.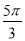
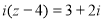 (i是虚数单位),则z的虚部为_______.
(i是虚数单位),则z的虚部为_______.