题目内容
已知α,β为锐角,tanα=| 1 |
| 7 |
| ||
| 10 |
分析:根据β为锐角,由sinβ的值,利用同角三角函数间的基本关系求出cosβ,即可求出tanβ的值,然后利用二倍角正切函数公式求出tan2β的值,且根据求出的tan2β的值判断出2β的范围,由tanα的值判断出α的范围,即可得到α+2β的范围,利用两角和的正切函数公式化简后,把tanα和tan2β的值代入即可求出tan(α+2β)值,然后根据α+2β的范围,利用特殊角的三角函数值即可求出α+2β的值.
解答:解:因为β为锐角,sinβ=
,所以cosβ=
,则tanβ=
,
而tan2β=
=
=
<1,得到0<2β<
,且tanα=
<
,得到0<α<
,
则tan(α+2β)=
=
=1,
由α,β为锐角,得到α+2β∈(0,
),所以α+2β=
.
| ||
| 10 |
3
| ||
| 10 |
| 1 |
| 3 |
而tan2β=
| 2tanβ |
| 1-tan2β |
2×
| ||
1-(
|
| 3 |
| 4 |
| π |
| 4 |
| 1 |
| 7 |
| ||
| 3 |
| π |
| 6 |
则tan(α+2β)=
| tanα+tan2β |
| 1-tanαtan2β |
| ||||
1-
|
由α,β为锐角,得到α+2β∈(0,
| 5π |
| 12 |
| π |
| 4 |
点评:此题考查学生灵活运用同角三角函数间的基本关系、二倍角的正切函数公式及两角和的正切函数公式化简求值,是一道综合题.学生做题时应注意角度的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC,如果对一切实数t,都有|
-
|≥|
|,则△ABC一定为( )
| BA |
| tBC |
| AC |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、与t的值有关 |
 ,
, ,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.
,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.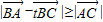 ,则△ABC一定为( )
,则△ABC一定为( )