题目内容
已知△ABC，如果对一切实数t，都有|
-
|≥|
|，则△ABC一定为（ ）
| BA |
| tBC |
| AC |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、与t的值有关 |
分析：则根据向量的减法的几何意义，由|
-
|≥|
|对一切实数t都成立可得|
|≥|
|可得AC⊥BC，从而可得
| BA |
| tBC |
| AC |
| AM |
| AC |
解答：解：令
=
-t
，则根据向量的减法的几何意义可得M在BC上
由|
-
|≥|
|对一切实数t都成立可得|
|≥|
|可得AC⊥BC
三角形为直角三角形
故选C
| AM |
| BA |
| BC |
由|
| BA |
| tBC |
| AC |
| AM |
| AC |
三角形为直角三角形
故选C
点评：本题是一道构造非常巧妙的试题，解题的关键是由|
-
|≥|
|对一切实数t都成立可得到AC为A到BC的距离．
| BA |
| tBC |
| AC |
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
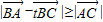，则△ABC一定为
，则△ABC一定为（ ）
|≥|
|，则△ABC一定为