题目内容
定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b= mq-np,下面说法错误的是 A.若a与b共线,则a⊙b =0 B.a⊙b =b⊙a
C.对任意的 R,有(
R,有(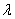 a)⊙b =
a)⊙b =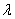 (a⊙b) D.(a⊙b)2+(a·b)2= |a|2|b|2
(a⊙b) D.(a⊙b)2+(a·b)2= |a|2|b|2
B【解析】由定义知:a⊙b= mq-np:所以选项A正确;又b⊙a=pn-mq≠a⊙b= mq-np,所以选项B错误;(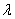 a)⊙b=
a)⊙b= ,
,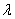 (a⊙b)=
(a⊙b)= 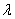 ( mq-np)=
( mq-np)=  所以对任意的
所以对任意的 R,有(
R,有(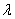 a)⊙b =
a)⊙b =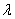 (a⊙b),选项C正确;(a⊙b)2+(a·b)2=( mq-np)2+( mp+nq)2=
(a⊙b),选项C正确;(a⊙b)2+(a·b)2=( mq-np)2+( mp+nq)2=  |a|2|b|2=
|a|2|b|2= ,所以(a⊙b)2+(a·b)2= |a|2|b|2,因此D正确。
,所以(a⊙b)2+(a·b)2= |a|2|b|2,因此D正确。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
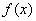 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当 时,
时, ,则满足
,则满足 的
的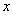 的取值范围是 ( )
的取值范围是 ( ) B.(1,+∞) C.
B.(1,+∞) C. D.(
D.( -1,+∞)
-1,+∞)  是偶函数,
是偶函数, 上是单调减函数,则
上是单调减函数,则 B.
B. C.
C. D.
D.
 ,其中常数a > 0.
,其中常数a > 0. 上是减函数;(2) 求函数f(x)的最小值.
上是减函数;(2) 求函数f(x)的最小值. 是实数.若函数
是实数.若函数 是定义在
是定义在 上的奇函数,但不是偶函数,则函数
上的奇函数,但不是偶函数,则函数 的递增区间为 .
的递增区间为 . ,
, .(Ⅰ)求函数
.(Ⅰ)求函数 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当 时,都有
时,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围. ABC中,
ABC中, ,
, ,面积为
,面积为 ,则
,则 的值为( )
的值为( ) D.
D.
 中,若
中,若 ,且
,且 ,则
,则 中,已知
中,已知 ,给出以下四个论断:①
,给出以下四个论断:①  ; ②
; ②  ;③
;③  ;④
;④