题目内容
16.过直线x+y-2$\sqrt{2}$=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,求点P的坐标.分析 求出圆心到直线的距离,利用两条切线的夹角是60°,设出P的终边,即可求解.
解答 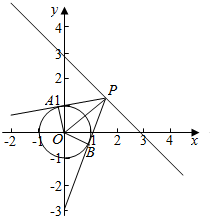 解:如图:由题意可知∠APB=60°,
解:如图:由题意可知∠APB=60°,
由切线性质可知∠OPB=30°,
在直角三角形OBP中,OP=2OB=2,又点P在直线x+y-2$\sqrt{2}$=0上,所以不妨设点P(x,2$\sqrt{2}-x$),
则OP=$\sqrt{{x}^{2}+(2\sqrt{2}-x)^{2}}=2$,即x2+(2$\sqrt{2}-x$)2=4,整理得x2-2$\sqrt{2}x$+2=0,解得x=$\sqrt{2}$,
即点P的坐标为($\sqrt{2}$,$\sqrt{2}$).
点评 本题考查直线与圆的位置关系的应用,圆的切线方程的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
11.若在△ABC中,∠A=30°,b=3,S△ABC=$\sqrt{3}$,则$\frac{a+b+c}{sinA+sinB+sinC}$=( )
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{21}}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $13\sqrt{2}$ |
8.定义在R的奇函数f(x),当x<0时,f(x)=-x2+x,则x>0时,f(x)等于( )
| A. | x2+x | B. | -x2+x | C. | -x2-x | D. | x2-x |
5.下列赋值语句正确的是( )
| A. | 3=M | B. | a+1=M | C. | M-1=a | D. | M=a+1 |
 中,
中, ,函数
,函数 在
在 处取得极值,则
处取得极值,则 _________.
_________.