题目内容
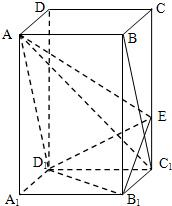
如图，若正四棱柱ABCD-A1B1C1D1的底面边长为2，高为4，则异面直线BD1与AD所成角的大小是分析：先通过平移将两条异面直线平移到同一个起点，得到的锐角或直角就是异面直线所成的角，在直角三角形中求出正切值，再用反三角函数值表示出这个角即可．
解答：
解：先画出图形
将AD平移到BC，则∠D1BC为异面直线BD1与AD所成角，
BC=2，D1C=2
，tan∠D1BC=
，
∴∠D1BC=arctan
，
故答案为arctan
．
解：先画出图形将AD平移到BC，则∠D1BC为异面直线BD1与AD所成角，
BC=2，D1C=2
| 5 |
| 5 |
∴∠D1BC=arctan
| 5 |
故答案为arctan
| 5 |
点评：本题主要考查了异面直线及其所成的角，以及解三角形的应用，属于基础题．
练习册系列答案
相关题目
如图，在正四棱柱ABCD-A1B1C1D1中，
如图，在正四棱柱ABCD-A1B1C1D1中，AB=a，AA1=2a，M、N分别是棱BB1，DD1的中点．
如图，在正四棱柱ABCD-A1B1C1D1中，已知AB=2，AA1=
（2008•奉贤区二模）如图，在正四棱柱ABCD-A1B1C1D1中，AB=4，AA1=8．
，M为棱A1A上的点，若A1C⊥平面MB1D1．