题目内容
(本题满分13分)
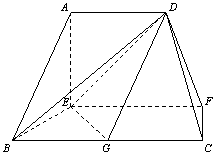
在如图的多面体中,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求二面角![]() 的余弦值.
的余弦值.
 |
解: (Ⅰ)证明:∵![]() ,
,
∴![]() .
.
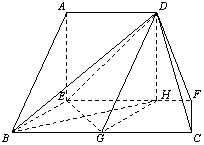 又∵
又∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴四边形![]() 是平行四边形, ∴
是平行四边形, ∴ ![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() .…………6分
.…………6分
(Ⅱ)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
 又
又![]() ,∴
,∴![]() 两两垂直. ……………………7分
两两垂直. ……………………7分
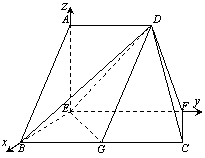
以点E为坐标原点,![]() 分别为
分别为![]() 轴建立如图的空间
轴建立如图的空间
直角坐标系.由已知得,![]() (0,0,2),
(0,0,2),![]() (2,0,0),
(2,0,0),
![]() (2,4,0),
(2,4,0),![]() (0,3,0),
(0,3,0),![]() (0,2,2),
(0,2,2),
![]() (2,2,0). …………………………8分
(2,2,0). …………………………8分
由已知得![]() 是平面
是平面![]() 的法向量. …………………9分
的法向量. …………………9分
设平面![]() 的法向量为
的法向量为![]() ,∵
,∵![]() ,
,
∴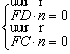 ,即
,即![]() ,令
,令![]() ,得
,得![]() . …………………11分
. …………………11分
设二面角![]() 的大小为
的大小为![]() ,
,
则![]() , ∴二面角
, ∴二面角![]() 的余弦值为
的余弦值为![]() ………13分
………13分

练习册系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.