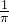题目内容
利用随机模拟方法可估计某无理数m的值,为此设计如图所示的程序框图,其中rand( )表示产生区间(0,1)上的随机数,P为s与n之比值,执行此程序框图,输出结果P是m的估计值,则m是( )
A.

B.

C.ln2
D.lg3
【答案】分析:根据已知中rand( )表示产生区间(0,1)上的随机数,它能随机产生区间(0,1)内的任何一个实数,及已知中的程序框图,根据几何概型计算出x,y任取(0,1)上的数时,求y< 的概率,结合随机模拟实验的频率约为概率,即可得到答案.
的概率,结合随机模拟实验的频率约为概率,即可得到答案.
解答: 解:执行此程序框图,输出结果P是:任取(0,1)上的两个数x,y,求y<
解:执行此程序框图,输出结果P是:任取(0,1)上的两个数x,y,求y< 的概率.
的概率.
∵x∈(0,1),y∈(0,1)对应的平面区域面积为:1×1=1,
而y< 对应的平面区域的面积为:
对应的平面区域的面积为: =ln2,
=ln2,
故任取(0,1)上的两个数x,y,y< 的概率P=
的概率P= =ln2
=ln2
执行此程序框图,输出结果P是m的估计值,则m是ln2,
故选C.
点评:本题考查的知识点是程序框图,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键.
 的概率,结合随机模拟实验的频率约为概率,即可得到答案.
的概率,结合随机模拟实验的频率约为概率,即可得到答案.解答:
 解:执行此程序框图,输出结果P是:任取(0,1)上的两个数x,y,求y<
解:执行此程序框图,输出结果P是:任取(0,1)上的两个数x,y,求y< 的概率.
的概率.∵x∈(0,1),y∈(0,1)对应的平面区域面积为:1×1=1,
而y<
 对应的平面区域的面积为:
对应的平面区域的面积为: =ln2,
=ln2,故任取(0,1)上的两个数x,y,y<
 的概率P=
的概率P= =ln2
=ln2执行此程序框图,输出结果P是m的估计值,则m是ln2,
故选C.
点评:本题考查的知识点是程序框图,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键.

练习册系列答案
相关题目
 某人利用随机模拟方法估计π的近似值,设计了下面的程序框图,运行时,从键盘输入1000,输出值为788,由此可估计π的近似值约为( )
某人利用随机模拟方法估计π的近似值,设计了下面的程序框图,运行时,从键盘输入1000,输出值为788,由此可估计π的近似值约为( ) (2013•香洲区模拟)利用随机模拟方法可估计某无理数m的值,为此设计如图所示的程序框图,其中rand( )表示产生区间(0,1)上的随机数,P为s与n之比值,执行此程序框图,输出结果P是m的估计值,则m是( )
(2013•香洲区模拟)利用随机模拟方法可估计某无理数m的值,为此设计如图所示的程序框图,其中rand( )表示产生区间(0,1)上的随机数,P为s与n之比值,执行此程序框图,输出结果P是m的估计值,则m是( ) 利用随机模拟方法可估计某无理数m的值,为此设计如图所示的程序框图,其中rand表示产生区间(0,1)上的随机数,P为s与n之比值,执行此程序框图,输出结果P是m的估计值,则m是
利用随机模拟方法可估计某无理数m的值,为此设计如图所示的程序框图,其中rand表示产生区间(0,1)上的随机数,P为s与n之比值,执行此程序框图,输出结果P是m的估计值,则m是