题目内容
某人利用随机模拟方法估计π的近似值，设计了下面的程序框图，运行时，从键盘输入1000，输出值为788，由此可估计π的近似值约为（ ）分析：先由试验结果知在以边长为2的正方形中随机取点1000次，所取之点在以正方形中心为圆心，1为半径的圆中的次数为788次，即所取的点在圆内的概率为
，又由几何概型概率计算公式，所取的点在圆内的概率为圆的面积比正方形的面积，即
，由二者相等即可估计π的值．
| 788 |
| 1000 |
| π |
| 4 |
解答：解：依题意，共产生了i=1000对（-1，1）的随机数（a，b），其中能使a2+b2≤1的共有m=788对
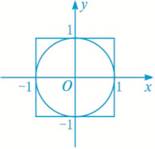
即在以边长为2的正方形中随机取点1000次，所取之点在以正方形中心为圆心，1为半径的圆中的次数为788次
设A={在以边长为2的正方形中随机取点，所取之点在以正方形中心为圆心，1为半径的圆中}
则P（A）=
=
，又由试验结果，P（A）=
=
∴
=
∴π=
=3.152．
故选C．
即在以边长为2的正方形中随机取点1000次，所取之点在以正方形中心为圆心，1为半径的圆中的次数为788次
设A={在以边长为2的正方形中随机取点，所取之点在以正方形中心为圆心，1为半径的圆中}
则P（A）=
| S圆 |
| S正方形 |
| π |
| 4 |
| m |
| i |
| 788 |
| 1000 |
∴
| π |
| 4 |
| 788 |
| 1000 |
∴π=
| 788×4 |
| 1000 |
故选C．
点评：本题考查了对算法的表示方法之一程序框图的认识，以及由框图反映出的几何概型概率的求法，随机模拟的方法求概率的过程．
练习册系列答案
相关题目
