题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,A=30°,若将一枚质地均匀的正方体骰子先后抛掷两次,所得的点数分别为a,b,则满足条件的三角形有两个解的概率是( )
A． | B． | C． | D． |
A
【思路点拨】先利用三角形有两解的条件求出a,b的范围,进而求出基本事件的个数,从而得出有两组解的所有事件及个数,利用古典概型即可求解.
解:要使△ABC有两个解,需满足的条件是
因为A=30°,所以
满足此条件的a,b的值有b=3,a=2;b=4,a=3;b=5,a=3;
b=5,a=4;b=6,a=4;b=6,a=5,共6种情况,所以满足条件的三角形有两个解的概率是
=.
解:要使△ABC有两个解,需满足的条件是
因为A=30°,所以
满足此条件的a,b的值有b=3,a=2;b=4,a=3;b=5,a=3;b=5,a=4;b=6,a=4;b=6,a=5,共6种情况,所以满足条件的三角形有两个解的概率是
=.
练习册系列答案
相关题目
表示编号为
的样品首轮同时被抽到的概率．
的值；
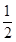
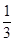
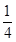
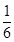
则(1)在出现点数有2的情况下,方程组只有一个解的概率为 .
