题目内容
20.设定义在(0,+∞)的函数f(x)的导函数是f'(x),且x4f'(x)+3x3f(x)=ex,$f(3)=\frac{e^3}{81}$,则x>0时,f(x)( )| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既无极大值,又无极小值 | D. | 既有极大值,又有极小值 |
分析 求出函数的导数,根据函数的单调性判断函数的极值即可.
解答 解:$f'(x)=\frac{{{e^x}-3{x^3}f(x)}}{x^4}$,
设h(x)=ex-3f(x)x3,
则h'(x)=ex-3[f'(x)x3+3f(x)x2]
=${e^x}-\frac{3}{x}[{f'(x){x^4}+3f(x){x^3}}]$
=${e^x}-\frac{3}{x}•{e^x}={e^x}•\frac{x-3}{x}$,
所以h(x)≥h(3)=e3-81f(3)=0,
即f'(x)≥0,因此f(x)在(0,+∞)递增,既无极大值,又无极小值,
故选:C.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.以A(1,3)和B(-5,1)为端点的线段AB的中垂线方程是( )
| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |
11.已知非零常数α是函数y=x+tanx的一个零点,则(α2+1)(1+cos2α)的值为( )
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
5.设i为虚数单位,复数$\frac{a+2i}{1+i}$为纯虚数,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
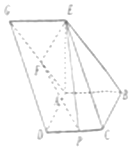 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.