题目内容
设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)>0,f(1)>0,求证:
(1)a>0且-2< <-1;
<-1;
(2)函数y=f(x)在(0,1)内有两个零点.
证明:(1)因为f(0)>0,f(1)>0,
所以c>0,3a+2b+c>0.
由条件a+b+c=0,消去b,得a>c>0;
由条件a+b+c=0,消去c,得a+b<0,
2a+b>0,故-2< <-1.
<-1.
(2)抛物线f(x)=3ax2+2bx+c的对称轴为x=-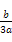 ,
,
在-2< <-1的两边乘以-
<-1的两边乘以- ,
,
得 <-
<-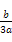 <
< .
.
又因为f(0)>0,f(1)>0,
又f(-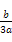 )=
)=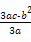
=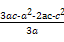
=-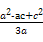
=-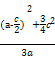 <0,
<0,
所以方程f(x)=0在区间(0,-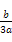 )与(-
)与(-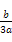 ,1)内分别有一实根.
,1)内分别有一实根.
故函数y=f(x)在(0,1)内有两个零点.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
已知函数y=f(x)的图象是连续不间断的曲线,且有如下的对应值:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 124.4 | 35 | -74 | 14.5 | -56.7 | -123.6 |
则函数y=f(x)在区间[1,6]上的零点至少有( )
(A)2个 (B)3个 (C)4个 (D)5个
 ,函数g(x)=
,函数g(x)= 则函数g(x)的最小值是 .
则函数g(x)的最小值是 . 



 且函数y=f(x)+ax恰有3个不同的零点,则实数a的取值范围是 .
且函数y=f(x)+ax恰有3个不同的零点,则实数a的取值范围是 . 
 x3-2x2+3x+1上任意一点,曲线在M处的切线为l,求:(1)斜率最小的切线方程;
x3-2x2+3x+1上任意一点,曲线在M处的切线为l,求:(1)斜率最小的切线方程;