题目内容
已知M={x||x-3|＜4}，N={x|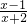
＜0，x∈Z}，则M∩N=
- A.?
- B.{0}
- C.{2}
- D.{x|2≤x≤7}
B
分析：利用绝对值不等式及分式不等式的解法，我们易求出集合M，N，再根据集合交集运算法则，即可求出答案．
解答：∵M={x||x-3|＜4}=（-1，7），
N={x|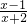＜0，x∈Z}={x|-2＜x＜1，x∈Z}={-1，0}，
∴M∩N={0}
故选B
点评：本题考查的知识点是交集及其运算，其中根据绝对值不等式及分式不等式的解法，求出集合M，N，是解答本题的关键．
分析：利用绝对值不等式及分式不等式的解法，我们易求出集合M，N，再根据集合交集运算法则，即可求出答案．
解答：∵M={x||x-3|＜4}=（-1，7），
N={x|
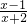＜0，x∈Z}={x|-2＜x＜1，x∈Z}={-1，0}，∴M∩N={0}
故选B
点评：本题考查的知识点是交集及其运算，其中根据绝对值不等式及分式不等式的解法，求出集合M，N，是解答本题的关键．
练习册系列答案
相关题目
)x＜2},N={x|log2x＜1},则M∩N等于
，则M∩N=（ ）