题目内容
2.如图,在Rt△BEC中,∠EBC=30°,∠BEC=90°,CE=1,现在分别以BE,CE为边向Rt△BEC外作正△EBA和正△CED.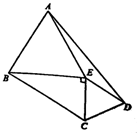
(Ⅰ)求线段AD的长;
(Ⅱ)比较∠ADC和∠ABC的大小.
分析 (Ⅰ)求出BE,AE=BE=$\sqrt{3}$,DE=CE=1,∠AED=150°,利用余弦定理求线段AD的长;
(Ⅱ)比较∠ADC和∠ABC的大小,转化为比较∠ADE与∠EBC的大小.
解答 解:(Ⅰ)在Rt△BEC中,CE=1,∠EBC=30°,∴BE=$\sqrt{3}$,
在△ADE中,AE=BE=$\sqrt{3}$,DE=CE=1,∠AED=150°,
由余弦定理可得AD=$\sqrt{3+1-2×\sqrt{3}×1×(-\frac{\sqrt{3}}{2})}$=$\sqrt{7}$;
(Ⅱ)∵∠ADC=∠ADE+60°,∠ABC=∠EBC+60°,
∴问题转化为比较∠ADE与∠EBC的大小.
在△ADE中,由正弦定理可得$\frac{sin∠ADE}{AE}=\frac{sin∠AED}{AD}$,
∴sin∠ADE=$\frac{\frac{1}{2}×\sqrt{3}}{\sqrt{7}}$<$\frac{1}{2}$=sin30°,
∴∠ADE<30°
∴∠ADC<∠ABC.
点评 本题考查余弦定理的运用,考查正弦定理,考查学生分析解决问题的能力,正确运用正弦、余弦定理是关键.

练习册系列答案
相关题目
12.阅读如图的程序框图,运行相应的程序,若输入x的值为2,则输出y的值为( )
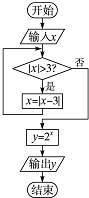

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
13.若函数f(x)=3|x-2|-m-2有唯一的零点,则直线mx+ky+3k-2=0恒过定点为( )
| A. | ($\frac{2}{7},-3$) | B. | (-2,-3) | C. | (0,$\frac{2}{7}$) | D. | (-2,0) |
17.已知f(x)=$\left\{\begin{array}{l}{2x+1,}&{x≤0}\\{{x}^{2}-1,}&{x>0}\end{array}\right.$,则“f[f(a)]=1“是“a=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
7.设a,b是空间中的两条不同的直线,α,β是两个不同的平面,则a⊥b的一个充分条件是( )
| A. | a?α,b⊥β,α∥β | B. | a⊥α,b⊥β,α∥β | C. | a∥α,b∥β,α⊥β | D. | a?α,b∥β,α⊥β |
14.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),且f(1)=2,则f(2015)的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
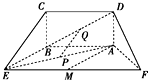 如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.
如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.