题目内容
10.对于函数y=f(x),x∈D,若对任意的x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x}_{1})f({x}_{2})}$=M,则称函数f(x)在D上的几何平均数为M,已知f(x)=x3-x2+1,x∈[1,2],则函数f(x)=x3-x2+1在[1,2]上的几何平均数M=$\sqrt{5}$.分析 根据已知中对于函数y=f(x),x∈D,若存在常数C,对任意x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x}_{1})f({x}_{2})}$=M,则称函数f(x)在D上的几何平均数为M.我们易得若函数在区间D上单调递增,则M应该等于函数在区间D上最大值与最小值的几何平均数,由f(x)=x3-x2+1,D=[1,2],代入即可得到答案.
解答 解:根据已知中关于函数f(x)在D上的几何平均数为M的定义,
由于f(x)的导数为f′(x)=3x2-2x,在{1,2]内f′(x)>0,
则f(x)=x3-x2+1在区间[1,2]单调递增,
则x1=1时,存在唯一的x2=2与之对应,
且x=1时,f(x)取得最小值1,x=2时,取得最大值5,
故M=$\sqrt{1×5}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题主要考查了应用新定义分析题意解决问题.对于新定义的问题,需要认真分析定义内容,切记不可偏离题目.

练习册系列答案
相关题目
20.设△ABC的内角A,B,C所对的边长分别为a,b,c,且atanB=$\frac{20}{3}$,bsinA=4,则a等于( )
| A. | 3 | B. | $\frac{8}{3}$ | C. | 4 | D. | 5 |
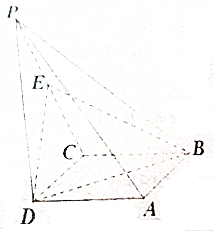 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.