题目内容
12．如图所示的程序框图所表示的算法功能是（ ）
| A． | 输出使1×2×4×…×n≥2015成立的最小整数n | |
| B． | 输出使1×2×4×…×n≥2015成立的最大整数n | |
| C． | 输出使1×2×4×…×n≥2015成立的最大整数n+2 | |
| D． | 输出使1×2×4×…×n≥2015成立的最小整数n+2 |
分析 写出经过几次循环得到的结果，得到求的s的形式，判断出框图的功能．
解答 解：经过第一次循环得到s=1×2，i=4
经过第二次循环得到s=1×2×4，i=6
经过第三次循环得到s=1×2×4×6，i=8
…
s=1×2×4×6×…×i≥2015，i=i+2，
该程序框图表示算法的功能是求计算并输出使1×2×4×6×…×i≥2015成立的最小整数n再加2，
故选：D．
点评 本题考查程序框图，考查了循环体以及循环次数两个具体问题，常采用写出前几次循环的结果，找规律，属于基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
3．化简复数$\frac{1+\sqrt{3}i}{1-i}$（其中i为虚数单位）的结果是（ ）
| A． | $\frac{1-\sqrt{3}}{2}$+$\frac{1+\sqrt{3}}{2}$i | B． | $\frac{1-\sqrt{3}}{2}$-$\frac{1+\sqrt{3}}{2}$i | C． | $\frac{1+\sqrt{3}}{2}$+$\frac{1-\sqrt{3}}{2}$i | D． | $\frac{1+\sqrt{3}}{2}$-$\frac{1-\sqrt{3}}{2}$i |
7．设命题p：函数f（x）=ex在R上为增函数；命题q：函数f（x）=cos2x为奇函数，则下列命题中真命题是（ ）
| A． | p∧q | B． | （￢p）∨q | C． | （￢p）∧（￢q） | D． | p∧（￢q） |
17．要制作一个容积为8m3，高为2m的无盖长方体容器，若容器的底面造价是每平方米200元，侧面造型是每平方米100元，则该容器的最低总造价为（ ）
| A． | 1200元 | B． | 2400元 | C． | 3600元 | D． | 3800元 |
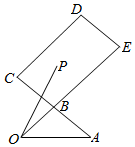如图，B是AC的中点，$\overrightarrow{BE}$=2$\overrightarrow{OB}$，P是矩形BCDE内（含边界）的一点，且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x，y∈R）．则x-y的最大值为-1．
1．若复数z满足1+z=i，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |