题目内容
17.要制作一个容积为8m3,高为2m的无盖长方体容器,若容器的底面造价是每平方米200元,侧面造型是每平方米100元,则该容器的最低总造价为( )| A. | 1200元 | B. | 2400元 | C. | 3600元 | D. | 3800元 |
分析 设长方体容器的长为xm,宽为ym;从而可得xy=4,从而写出该容器的造价为200xy+100(2x+2x+2y+2y)=800+400(x+y),再利用基本不等式求最值即可.
解答 解:设长方体容器的长为xm,宽为ym,
则x•y•2=8,
即xy=4,
则该容器的造价为:
z=200xy+100(2x+2x+2y+2y)
=800+400(x+y)
≥800+400×2$\sqrt{xy}$
=800+1600=2400.
(当且仅当x=y=2时,等号成立)
故该容器的最低总价是2400元.
故选:B.
点评 本题考查基本不等式在实际问题中的应用,考查化简的运算能力,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12.若四边形ABCD为菱形,则下列等式中成立的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{BA}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AC}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$ |
12.如图所示的程序框图所表示的算法功能是( )


| A. | 输出使1×2×4×…×n≥2015成立的最小整数n | |
| B. | 输出使1×2×4×…×n≥2015成立的最大整数n | |
| C. | 输出使1×2×4×…×n≥2015成立的最大整数n+2 | |
| D. | 输出使1×2×4×…×n≥2015成立的最小整数n+2 |
2. 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
 某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )
某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中$\overline{a}$是这7个数据的平均数),则输出的S的值是( )| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
| A. | 1 | B. | $\frac{8}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{10}{7}$ |
7.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点分别为F1,F2,O为坐标原点,以OF2为直径的圆交双曲线于A,B两点,若△F1AB的外接圆过点($\frac{4\sqrt{{a}^{2}+{b}^{2}}}{5}$,0),则该双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
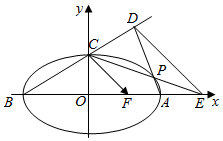 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.