题目内容
已知函数f(x)=(cos x-x)(π+2x)-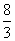 (sin x+1),g(x)=3(x-π)cos x-4(1+sin x)ln
(sin x+1),g(x)=3(x-π)cos x-4(1+sin x)ln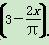 .证明:
.证明:
(1)存在唯一x0∈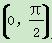 ,使f(x0)=0;
,使f(x0)=0;
(2)存在唯一x1∈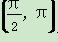 ,使g(x1)=0,且对(1)中的x0,有x0+x1<π.
,使g(x1)=0,且对(1)中的x0,有x0+x1<π.
证明:(1)当x∈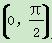 时,f′(x)=-(1+sin x)·(π+2x)-2x-
时,f′(x)=-(1+sin x)·(π+2x)-2x- cos x<0,函数f(x)在
cos x<0,函数f(x)在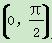 上为减函数.又f(0)=π-
上为减函数.又f(0)=π-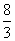 >0,f
>0,f =-π2-
=-π2- <0,所以存在唯一x0∈
<0,所以存在唯一x0∈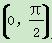 ,使f(x0)=0.
,使f(x0)=0.
(2)记函数 令t=π-x,则当
令t=π-x,则当
因为x1=π-t1,t1>x0,所以x0+x1<π.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 ,则函数
,则函数 的零点的个数为_______个.
的零点的个数为_______个.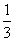 ,求B.
,求B. .
.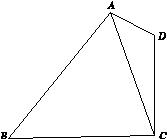
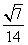 ,sin∠CBA=
,sin∠CBA=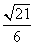 ,求BC的长.
,求BC的长.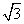 ,cos2A-cos2B=
,cos2A-cos2B=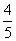 ,求△ABC的面积.
,求△ABC的面积. -sin2x.
-sin2x. 的值;
的值; ,都有f(x)≤c,求实数c的取值范围.
,都有f(x)≤c,求实数c的取值范围. 在
在 时有最大值
时有最大值 ,求
,求 的值
的值 ,b=
,b= 为不等式组
为不等式组 表示的平面区域
表示的平面区域 之间的距离的最小值为______.
之间的距离的最小值为______.