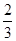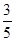题目内容
设 是正三棱锥,
是正三棱锥, 是
是 的重心,
的重心, 是
是 上的一点,且
上的一点,且 ,若
,若 ,则
,则 为( )
为( )
A. | B. | C. | D. |
A
解析试题分析:由 是
是 上一点,且
上一点,且 ,可得
,可得
又因为 是
是 的重心,所以
的重心,所以


而 ,所以
,所以 ,所以
,所以 ,选A.
,选A.
考点:1.空间向量的加减法;2.空间向量的基本定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 , 则
, 则 两点间距离的最小值是( )
两点间距离的最小值是( )
A. | B.2 | C. | D.1 |
已知正方体 的棱长为
的棱长为 ,
, ,点N为
,点N为 的中点,则
的中点,则 ( )
( )
A. | B. | C. | D. |
设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若 =x
=x +y
+y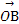 +z
+z ,则(x,y,z)为( )
,则(x,y,z)为( )
A.( , , , , ) ) | B.( , , , , ) ) |
C.( , , , , ) ) | D.( , , , , ) ) |
如图,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN= ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).
| A.相交 | B.平行 | C.垂直 | D.不能确定 |
 中,底面ABC为直角三角形,
中,底面ABC为直角三角形, ,
, . 已知G与E分别为
. 已知G与E分别为 和
和 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和 上的动点(不包括端点). 若
上的动点(不包括端点). 若 ,则线段
,则线段 的长度的最小值为 。
的长度的最小值为 。