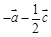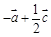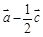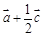题目内容
已知向量m=(2cosx, cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+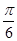 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.
(1)求函数y=f(x)的单调递增区间;
(2)设△ABC的内角A满足f(A)=2,a、b、c分别为角A、B、C所对的边,且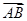 ·
·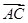 =
= ,求边BC的最小值.
,求边BC的最小值.
 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+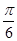 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.(1)求函数y=f(x)的单调递增区间;
(2)设△ABC的内角A满足f(A)=2,a、b、c分别为角A、B、C所对的边,且
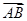 ·
·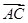 =
= ,求边BC的最小值.
,求边BC的最小值.(1)[kπ-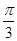 ,kπ+
,kπ+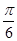 ](k∈Z)
](k∈Z)
(2) -1
-1
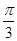 ,kπ+
,kπ+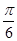 ](k∈Z)
](k∈Z)(2)
 -1
-1解:(1)f(x)=2cosx(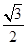 sinx+
sinx+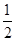 cosx)+
cosx)+ sinx·cosx-sin2x=2
sinx·cosx-sin2x=2 sinx·cosx+cos2x-sin2x=
sinx·cosx+cos2x-sin2x= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+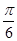 ),
),
由2kπ-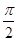 ≤2x+
≤2x+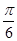 ≤2kπ+
≤2kπ+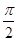 ,k∈Z,
,k∈Z,
得kπ-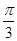 ≤x≤kπ+
≤x≤kπ+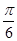 ,k∈Z,
,k∈Z,
故所求单调递增区间为[kπ-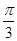 ,kπ+
,kπ+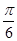 ](k∈Z).
](k∈Z).
(2)由f(A)=2sin(2A+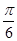 )=2,
)=2,
0<A<π得A=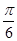 ,
,
∵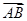 ·
·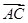 =
= ,即bccosA=
,即bccosA= ,
,
∴bc=2,
又△ABC中,
a2=b2+c2-2bccosA=b2+c2- bc≥2bc-
bc≥2bc- bc=(2-
bc=(2- )bc,
)bc,
∴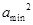 =(2-
=(2- )×2=4-2
)×2=4-2 ,
,
∴amin=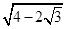 =
= -1.
-1.
即边BC的最小值为 -1.
-1.
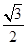 sinx+
sinx+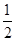 cosx)+
cosx)+ sinx·cosx-sin2x=2
sinx·cosx-sin2x=2 sinx·cosx+cos2x-sin2x=
sinx·cosx+cos2x-sin2x= sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+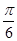 ),
),由2kπ-
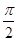 ≤2x+
≤2x+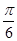 ≤2kπ+
≤2kπ+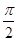 ,k∈Z,
,k∈Z,得kπ-
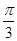 ≤x≤kπ+
≤x≤kπ+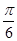 ,k∈Z,
,k∈Z,故所求单调递增区间为[kπ-
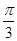 ,kπ+
,kπ+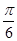 ](k∈Z).
](k∈Z).(2)由f(A)=2sin(2A+
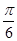 )=2,
)=2,0<A<π得A=
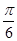 ,
,∵
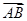 ·
·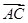 =
= ,即bccosA=
,即bccosA= ,
,∴bc=2,
又△ABC中,
a2=b2+c2-2bccosA=b2+c2-
 bc≥2bc-
bc≥2bc- bc=(2-
bc=(2- )bc,
)bc,∴
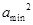 =(2-
=(2- )×2=4-2
)×2=4-2 ,
,∴amin=
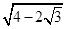 =
= -1.
-1.即边BC的最小值为
 -1.
-1.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
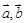 满足
满足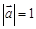 ,且
,且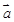 与
与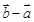 的夹角为
的夹角为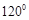 ,则
,则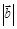 的取值范围为 。
的取值范围为 。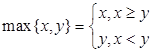 ,
, ,设
,设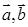 为平面向量,则( )
为平面向量,则( )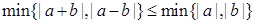
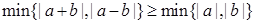
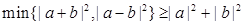
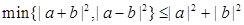
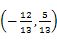 ,θ为a与b的夹角.
,θ为a与b的夹角.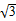 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间.  ,则
,则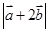 的值为 .
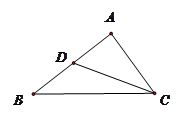
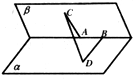
的值为 .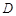 是
是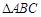 的边
的边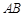 上的中点,记
上的中点,记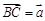 ,
,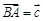 ,则向量
,则向量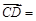 ( ).
( ).