题目内容
(2014·黄冈模拟)设a=(cosα,sinα),b=(cosβ,sinβ),若a-b=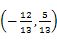 ,θ为a与b的夹角.
,θ为a与b的夹角.
(1)求θ的值.
(2)若f(x)=2sin(θ-x)cos(θ-x)+2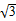 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间.
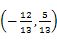 ,θ为a与b的夹角.
,θ为a与b的夹角.(1)求θ的值.
(2)若f(x)=2sin(θ-x)cos(θ-x)+2
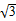 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间. (1) (2)
(2) ,k∈Z.
,k∈Z.
 (2)
(2) ,k∈Z.
,k∈Z.(1)由题意:
两式平方相加得:2-2cos(α-β)=1,
所以cos(α-β)= ,
,
又cosθ=
=cosαcosβ+sinαsinβ
=cos(α-β)= ,
,
因为θ∈[0,π],所以θ= .
.
(2)f(x)=2sin(θ-x)cos(θ-x)+2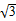 sin2(θ-x)
sin2(θ-x)
=-2sin +
+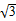 ,
,
令2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,
解得:kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
所以f(x)的单调递增区间为 ,k∈Z.
,k∈Z.

两式平方相加得:2-2cos(α-β)=1,
所以cos(α-β)=
 ,
,又cosθ=

=cosαcosβ+sinαsinβ
=cos(α-β)=
 ,
,因为θ∈[0,π],所以θ=
 .
.(2)f(x)=2sin(θ-x)cos(θ-x)+2
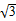 sin2(θ-x)
sin2(θ-x)=-2sin
 +
+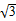 ,
,令2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,
,k∈Z,解得:kπ+
 ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,所以f(x)的单调递增区间为
 ,k∈Z.
,k∈Z.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+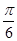 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n.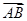 ·
·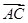 =
=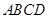 中,
中,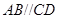 ,
,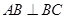 ,
,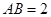 ,
,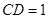 ,
,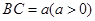 ,P为线段
,P为线段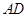 (含端点)上一个动点,设
(含端点)上一个动点,设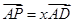 ,
,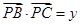 ,对于函数
,对于函数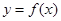 ,给出以下三个结论:①当
,给出以下三个结论:①当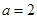 时,函数
时,函数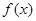 的值域为
的值域为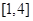 ;②对任意
;②对任意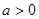 ,都有
,都有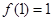 成立;③对任意
成立;③对任意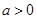 ,使得函数
,使得函数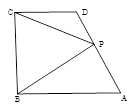
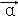 和
和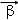 ,定义
,定义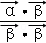 ,若平面向量
,若平面向量 、
、 满足|
满足|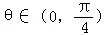 ,且
,且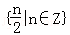 中,则
中,则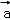 ○
○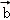 =( )
=( )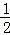
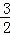
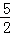
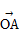 =a,
=a,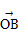 =b,且BC⊥OA,C为垂足,若
=b,且BC⊥OA,C为垂足,若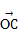 =λa(λ≠0),则λ=( )
=λa(λ≠0),则λ=( )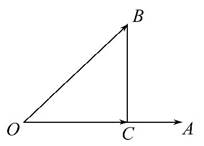
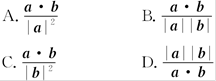
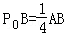 ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有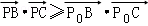 则( )
则( )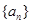 是公比为
是公比为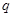 的无穷等比数列,下列
的无穷等比数列,下列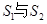 ;②
;②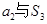 ;③
;③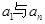 ;④
;④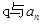 .
.  ,则
,则 的取值范围为( )
的取值范围为( ) B.
B. C
C D
D
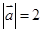 ,
,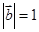 ,
,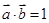 ,则向量
,则向量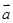 与
与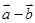 的夹角为 .
的夹角为 .