题目内容
已(12分)知椭圆的中心在坐标原点,离心率为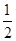 ,一个焦点是F(0,1).
,一个焦点是F(0,1).
(Ⅰ)求椭圆方程;
(Ⅱ)直线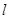 过点F交椭圆于A、B两点,且
过点F交椭圆于A、B两点,且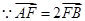 ,求直线
,求直线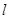 的方程.
的方程.
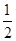 ,一个焦点是F(0,1).
,一个焦点是F(0,1).(Ⅰ)求椭圆方程;
(Ⅱ)直线
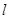 过点F交椭圆于A、B两点,且
过点F交椭圆于A、B两点,且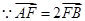 ,求直线
,求直线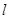 的方程.
的方程.(Ⅰ) .(Ⅱ)
.(Ⅱ) .
.
 .(Ⅱ)
.(Ⅱ) .
.试题分析: (1)根据已知中的条件得到离心率和a的关系式,进而得到椭圆的方程。
(2)对于直线斜率是否存在要给予讨论,并联立方程组的思想,结合韦达定理和向量关系式得到k的方程,求解得到k的值。
解:(Ⅰ)设椭圆方程为
 (
( >b>0).
>b>0).依题意,
 , c=1,
, c=1, ,
, ,………………………………2分
,………………………………2分∴所求椭圆方程为
 .………4分
.………4分(Ⅱ)若直线
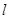 的斜率k不存在,则不满足
的斜率k不存在,则不满足 .
. 当直线
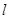 的斜率k存在时,设直线
的斜率k存在时,设直线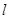 的方程为
的方程为 .因为直线
.因为直线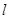 过椭圆的焦点F(0,1),所以
过椭圆的焦点F(0,1),所以 取任何实数, 直线
取任何实数, 直线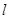 与椭圆均有两个交点A、B.
与椭圆均有两个交点A、B.设A

联立方程
 消去y,
消去y,得
 .…………6分
.…………6分 , ①
, ①  , ②
, ②由F(0,1),A
 ,
,则
 ,
,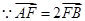 ,∴
,∴ ,
,得
 .……………………8分
.……………………8分将
 代入①、②,
代入①、②,得
 , ③
, ③  , ④……………10分
, ④……………10分由③、④ 得,

 ,
,化简得

 ,解得
,解得 ,
, .∴直线
.∴直线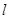 的方程为:
的方程为: .12分
.12分点评:解决该试题的关键是熟练掌握椭圆的几何性质,根据其性质得到参数a,b的值,进而得到其方程。同时联立方程组,结合向量的关系式和韦达定理得到从那数k的值。

练习册系列答案
相关题目
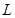 交抛物线
交抛物线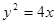 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是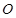 .
.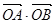 为定值;
为定值;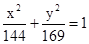 有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.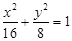 的焦点分别为
的焦点分别为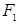 、
、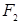 ,以原点为圆心且过焦点的圆O与椭圆相交于点
,以原点为圆心且过焦点的圆O与椭圆相交于点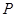 ,则
,则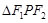 的面积等于( )
的面积等于( )



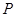 是圆
是圆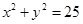 上的动点,点D是
上的动点,点D是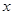 轴上的投影,M为
轴上的投影,M为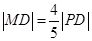
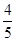 的直线被C所截线段的长度。
的直线被C所截线段的长度。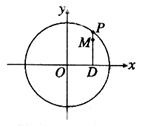
 仅有一个公共点的直线
仅有一个公共点的直线 的方程.
的方程.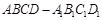 的棱长为
的棱长为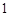 ,点
,点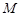 在棱
在棱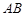 上, 且
上, 且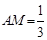 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点 的距离与点
的距离与点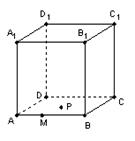
 为何值时,直线
为何值时,直线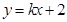 和曲线
和曲线 有两个公共点?有一个公共点?
有两个公共点?有一个公共点?