题目内容
 如图所示,O为坐标原点,在y轴上截距为2且斜率为k(k<0)的直线l与抛物线y2=2x交于M、N两点
如图所示,O为坐标原点,在y轴上截距为2且斜率为k(k<0)的直线l与抛物线y2=2x交于M、N两点
(1)求抛物线的焦点F的坐标;
(2)若 •
• =0,求直线l的方程;
=0,求直线l的方程;
(3)若点M、N将抛物线分成三段,在含有坐标原点的那一段上求一点P,使得△PMN的面积最大.
 解:(1)由题意,知p=1,所以抛物线的焦点坐标为:
解:(1)由题意,知p=1,所以抛物线的焦点坐标为: …(2分)
…(2分)(2)令直线l的方程为:y=kx+2…(1分)
设M(x1,y1)、N(x2,y2),
 消去y得,k2x2+(4k-2)x+4=0…(1分)
消去y得,k2x2+(4k-2)x+4=0…(1分) 解得k<0…①…(1分)
解得k<0…①…(1分) …(1分)
…(1分)由
 得,x1x2+y1y2=0
得,x1x2+y1y2=0即
 ,解得m=-1满足条件①…(1分)
,解得m=-1满足条件①…(1分)所以直线l的方程为:x+y-2=0…(1分)
(3)所以直线l′与抛物线相切与已知直线l平行,则令l′:y=kx+b…(1分)
 …(1分)
…(1分)消去y得,k2x2+2(bk-1)x+b2=0
由

 …(1分)
…(1分)由
 消去x得
消去x得 (k<0)
(k<0)解得
 代入
代入 得x=
得x= ,所以
,所以
所求的点P的坐标与直线l的斜率有关,其横坐标是直线l斜率的平方的两倍的倒数,纵坐标是直线l斜率的倒数.…(1分)
分析:(1)由抛物线的标准方程可直接求出抛物线的焦点F的坐标;
(2)令直线l的方程为:y=kx+2,与抛物线方程联立
 消去y得,k2x2+(4k-2)x+4=0,所以有
消去y得,k2x2+(4k-2)x+4=0,所以有 解得k<0,设M(x1,y1)、N(x2,y2),则有
解得k<0,设M(x1,y1)、N(x2,y2),则有 ,由
,由 得,x1x2+y1y2=0,从而可求满足条件的直线l的方程;
得,x1x2+y1y2=0,从而可求满足条件的直线l的方程;(3)所以直线l′与抛物线相切与已知直线l平行,则令l′:y=kx+b,与抛物线方程联立
 ,消去y得,k2x2+2(bk-1)x+b2=0,则
,消去y得,k2x2+2(bk-1)x+b2=0,则
 ,进而由
,进而由 消去x得
消去x得 ,即可求得点P的坐标.
,即可求得点P的坐标.点评:本题以抛物线为载体,考查抛物线的几何性质,考查向量知识的运用,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图所示,O为坐标原点,在y轴上截距为2且斜率为k(k<0)的直线l与抛物线y2=2x交于M、N两点
如图所示,O为坐标原点,在y轴上截距为2且斜率为k(k<0)的直线l与抛物线y2=2x交于M、N两点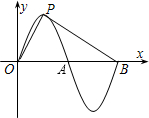 函数y=sinπx的部分图象如图所示,O为坐标原点,P是图象的最高点,A、B分别是图象与x轴的两交点,则tan∠APB等于( )
函数y=sinπx的部分图象如图所示,O为坐标原点,P是图象的最高点,A、B分别是图象与x轴的两交点,则tan∠APB等于( )
 =2x于M(x
=2x于M(x ,y
,y ,y
,y