题目内容
(本小题共13分)设数列 的前
的前 项和
项和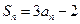
 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)若
 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和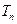
 的前
的前 项和
项和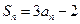
 .
.(Ⅰ)证明数列
 是等比数列;
是等比数列;(Ⅱ)若

 ,且
,且 ,求数列
,求数列 的前
的前 项和
项和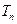
(Ⅰ)证:因为 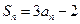
 ,
,
 ,
,
所以当 时,
时, ,整理得
,整理得 .
.
由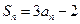 ,令
,令 ,得
,得 ,解得
,解得 .
.
所以 是首项为
是首项为 ,公比是
,公比是 的等比数列.…………6分
的等比数列.…………6分
(Ⅱ)解 :由
:由 ,得
,得 .
.
所以

从而 .
.
 .…………13分
.…………13分
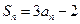
 ,
,
 ,
,所以当
 时,
时, ,整理得
,整理得 .
.由
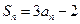 ,令
,令 ,得
,得 ,解得
,解得 .
.所以
 是首项为
是首项为 ,公比是
,公比是 的等比数列.…………6分
的等比数列.…………6分(Ⅱ)解
 :由
:由 ,得
,得 .
.所以

从而
 .
. .…………13分
.…………13分略

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ,数列
,数列 是以3为公比的等比数列,则
是以3为公比的等比数列,则 ( )
( ) 中,
中, ,则
,则 ( )
( )



 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有  .函数
.函数 ,数列
,数列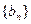 的首项
的首项 .
. 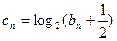 求证:
求证: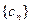 是等比数列并求
是等比数列并求 ,
, ,求数列
,求数列 的前n项和
的前n项和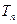 .
. 的前
的前 项和为
项和为 ,已知
,已知 成等差数列.
成等差数列. ;
; ,问
,问 是数列
是数列 的项构成的新数列
的项构成的新数列 是公比为
是公比为 的等比数
的等比数 列,则相应的数列
列,则相应的数列 是公比为
是公比为 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列 ,
, ,且
,且 .
. 项和
项和
 的前
的前 项和为
项和为 ,若
,若 ,则
,则
 ,则其前
,则其前 项和
项和 .
. ,己知
,己知 ,且满足
,且满足 ,则该医院30天内因患H
,则该医院30天内因患H 1N1流感就诊的人
1N1流感就诊的人 数共有
数共有