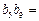题目内容
(本小题满分12分)已知各项均为正数的数列 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有  .函数
.函数 ,数列
,数列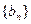 的首项
的首项 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令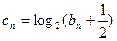 求证:
求证: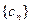 是等比数列并求
是等比数列并求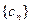 通项公式;
通项公式;
(Ⅲ)令 ,
, ,求数列
,求数列 的前n项和
的前n项和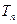 .
.
 中,
中, 是数列
是数列 的前
的前 项和,对任意
项和,对任意 ,有
,有  .函数
.函数 ,数列
,数列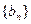 的首项
的首项 .
. (Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)令
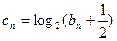 求证:
求证: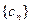 是等比数列并求
是等比数列并求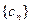 通项公式;
通项公式; (Ⅲ)令
 ,
, ,求数列
,求数列 的前n项和
的前n项和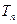 .
.解: (Ⅰ)由 ①
①
得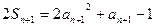 ②
②
由②—①,得
即: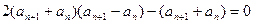 ---------2分
---------2分
 由于数列
由于数列 各项均为正数,
各项均为正数,
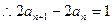
即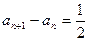
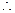 数列
数列 是首项为
是首项为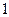 ,公差为
,公差为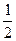 的等差数列,
的等差数列,
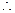 数列
数列 的通项公式是
的通项公式是 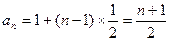 ----------4分
----------4分
(Ⅱ)由 知
知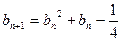 ,
,
所以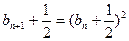 ,
,
有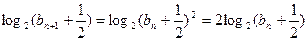 ,即
,即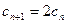 ,---------6分
,---------6分
而 ,
,
故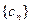 是以
是以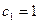 为首项,公比为2的等比数列。
为首项,公比为2的等比数列。
所以 ---------8分
---------8分
(Ⅲ)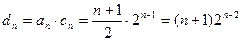 ,
,
所以数列 的前n项和
的前n项和
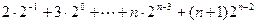
错位相减可得
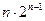 -----12分
-----12分
 ①
①得
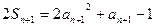 ②
② 由②—①,得

即:
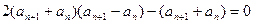 ---------2分
---------2分 由于数列
由于数列 各项均为正数,
各项均为正数,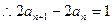
即
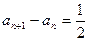
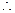 数列
数列 是首项为
是首项为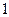 ,公差为
,公差为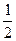 的等差数列,
的等差数列,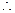 数列
数列 的通项公式是
的通项公式是 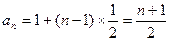 ----------4分
----------4分(Ⅱ)由
 知
知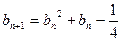 ,
,所以
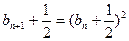 ,
, 有
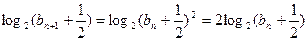 ,即
,即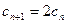 ,---------6分
,---------6分而
 ,
,故
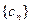 是以
是以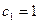 为首项,公比为2的等比数列。
为首项,公比为2的等比数列。 所以
 ---------8分
---------8分(Ⅲ)
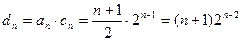 ,
, 所以数列
 的前n项和
的前n项和
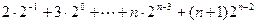
错位相减可得

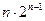 -----12分
-----12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,若
中,若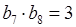 ,则
,则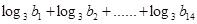 等于( )
等于( )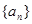 是等比数列,且
是等比数列,且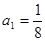 ,
,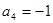 ,则数列
,则数列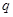 为( )
为( )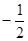
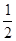
 的前
的前 项和
项和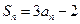
 .
.
 ,且
,且 ,求数列
,求数列 的前
的前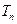
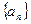 中, 若
中, 若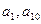 是方程
是方程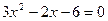 的两根,则
的两根,则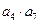 =_______
=_______ 是等比数列,
是等比数列, ,则公比
,则公比 等于
等于  中,
中, ,
, ,则
,则 =( )
=( )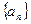 ,公比
,公比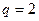 ,且
,且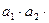
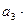 …
…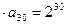 ,
,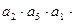 …
…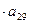 =__________.
=__________.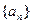 满足
满足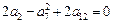 ,且数列
,且数列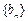 是等比数列,若
是等比数列,若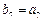 ,则
,则