题目内容
已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π.若f(x)的最小正周期为6π,且当x=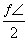 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A.f(x)在区间[-2π,0]上是增函数
B.f(x)在区间[-3π,-π]上是增函数
C.f(x)在区间[3π,5π]上是减函数
D.f(x)在区间[4π,6π]上是减函数
A
解析:∵f(x)的最小正周期为6π,∴ω= ,
,
∵当x=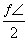 时,f(x)有最大值,
时,f(x)有最大值,
∴ ×
×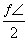 +φ=
+φ=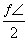 +2kπ(k∈Z),φ=
+2kπ(k∈Z),φ= +2kπ,
+2kπ,
∵-π<φ≤π,∴φ= .
.
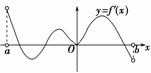
∴f(x)=2sin  ,由此函数图象易得,在区间[-2π,0]上是增函数,而在区间[-3π,-π]或[3π,5π]上均没单调性,在区间[4π,6π]上是单调增函数.
,由此函数图象易得,在区间[-2π,0]上是增函数,而在区间[-3π,-π]或[3π,5π]上均没单调性,在区间[4π,6π]上是单调增函数.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
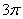 ,圆心角为
,圆心角为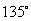 的扇形的半径为 ,面积为 .
的扇形的半径为 ,面积为 . ,且
,且 <α<
<α< ,则cos α-sin α的值是________.
,则cos α-sin α的值是________. ,直线
,直线 和
和 是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( )
是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴,则φ=( ) B.
B. C.
C. D.
D.

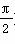 )的最小正周期是π,且f(0)=
)的最小正周期是π,且f(0)=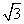 ,则( ).
,则( ).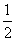 ,φ=
,φ=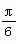 B.ω=
B.ω=
 ,sin β=
,sin β= ,则α+β= ( ).
,则α+β= ( ). B.
B. 
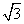 千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.
千米的C,D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两目标A,B之间的距离.