Question

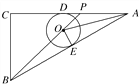
【题目】如图，在△ABC中，∠C＝90°，AC＝8 cm，AB＝10 cm，点P由C出发以每秒2 cm的速度沿线段CA向点A运动(不运动至A点)，⊙O的圆心在BP上，且⊙O分别与AB、AC相切，当点P运动2 s时，⊙O的半径是(　　)

A. cm B. cm C. cm D. 2 cm

Answer 1

【答案】A

【解析】∵PC＝2×2＝4 cm，

∴P是AC的中点，

∴BC＝6 cm，BP＝2 cm.连接OD，∵D为切点，

∴OD⊥AC，则OD∥BC，

即.设半径OD＝3k，DP＝2k，

∴，

∴.

∵AE、AD为⊙O的切线，

∴AE＝AD＝AP＋PD＝4＋2k，

BE＝10－(4＋2k)＝6－2k.

在Rt△BOE中，∵OB2＝BE2＋OE2，

∴，解得.

故半径OD＝3k＝.

本题选择A选项.