题目内容
7.将一个白球、一个黄球、两个红球(除颜色外完全相同)分给三个小朋友,且每个小朋友至少分得一个球的分法有21种.分析 把4个小球分成(2,1,1)组,其中2个小球分给同一个小朋友的有4种方法(红红,红黄,红白,白黄),分两类,根据分类计数原理可得.
解答 解:把4个小球分成(2,1,1)组,其中2个小球分给同一个小朋友的有4种方法(红红,红黄,红白,白黄),
若(红红,红黄,红白)分给其中一个小朋友,则剩下的两个球分给2个小朋友,共有3×3×A22=18种,
若(白黄两个小球)分给其中一个小朋友,剩下的两个红色小球只有1种分法,故有3×1=3种,
根据分类计数原理可得,共有18+3=21种.
故答案为:21.
点评 本题考查了分组分配的问题,关键是分组,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
19.若复数z满足z(1-i)=i2017(i是虚数单位),则复数z等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | -$\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
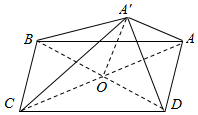 平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.
平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB. 如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.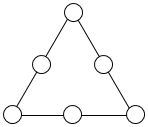 如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.
如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.