题目内容
7．设集合A={x|y=$\sqrt{16-{x}^{2}}$}，B={x|$\frac{lo{g}_{2}x}{2-lo{g}_{2}x}$≥0}，则A∩B=（ ）| A． | [1，4] | B． | [1，4） | C． | [1，2] | D． | （1，2] |
分析 通过函数的定义域求得集合A，解指数不等式求得集合B，再进行交集运算即可．
解答 解：∵16-x2≥0，
∴-4≤x≤4，
∴A=[-4，4]，
∵$\frac{lo{g}_{2}x}{2-lo{g}_{2}x}$≥0
∴log2x（log2x-2）≤0，且log2x-2≠0，
∴0≤log2x＜2，
∴1≤x＜4，
∴B=[1，4），
∴A∩B=[1，4）．
故选：B．
点评 本题考查交集及其运算，关键根据函数的定义域和对数函数的性质求出集合A，B，属于基础题．
练习册系列答案
相关题目
18．等比数列{an}的公比q＞0，已知a2=1，a4=4，则{an}的公比q的值为（ ）
| A． | -2 | B． | 1 | C． | 3 | D． | 2 |
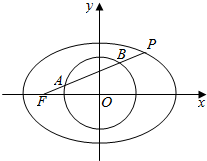如图，过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F作直线与圆x2+y2=$\frac{{a}^{2}}{4}$及椭圆依次交于点A、B、P，若FA=PB，且AB=$\frac{\sqrt{3}a}{2}$，则椭圆的离心率为$\frac{\sqrt{10}}{4}$．
16．甲、乙、丙、丁四人排成一排，其中甲、乙两人相邻的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{6}$ |