题目内容
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率e=
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率e=| 1 |
| 2 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)与圆(x+1)2+y2=1相切的直线l:y=kx+t交椭圆于M,N两点,若椭圆上一点C满足
| OM |
| ON |
| OC |
分析:(Ⅰ) 设椭圆的标准方程为
+
=1(a>b>0),由已知得
,解出即可求得a,b;
(Ⅱ)由直线l:y=kx+t与圆(x+1)2+y2=1相切,可得k,t的关系式①,把y=kx+t代入
+
=1消掉y得x的二次方程,设M(x1,y1),N(x2,y2),由
+
=λ
得λ
=(x1+x2,y1+y2),代入韦达定理可求得C点坐标,把点C代入椭圆方程可用k,t表示出λ,再由①式消掉k得关于t的函数,由t2范围可求得λ2的范围,进而求得λ的范围;
| x2 |
| a2 |
| y2 |
| b2 |
|
(Ⅱ)由直线l:y=kx+t与圆(x+1)2+y2=1相切,可得k,t的关系式①,把y=kx+t代入
| x2 |
| 16 |
| y2 |
| 12 |
| OM |
| ON |
| OC |
| OC |
解答:解:(Ⅰ) 设椭圆的标准方程为
+
=1(a>b>0),
由已知得:
,解得
,
所以椭圆的标准方程为:
+
=1;
(Ⅱ) 因为直线l:y=kx+t与圆(x+1)2+y2=1相切,
所以
=1⇒2k=
(t≠0),
把y=kx+t代入
+
=1并整理得:(3+4k2)x2+8ktx+(4t2-48)=0,
设M(x1,y1),N(x2,y2),则有x1+x2=-
,y1+y2=kx1+t+kx2+t=k(x1+x2)+2t=
,
因为λ
=(x1+x2,y1+y2),
所以C(
,
),
又因为点C在椭圆上,
所以
+
=1⇒λ2=
=
,
因为t2>0,所以 (
)2+(
)+1>1,
所以0<λ2<1,
所以λ的取值范围为(-1,0)∪(0,1).
| x2 |
| a2 |
| y2 |
| b2 |
由已知得:
|
|
所以椭圆的标准方程为:
| x2 |
| 16 |
| y2 |
| 12 |
(Ⅱ) 因为直线l:y=kx+t与圆(x+1)2+y2=1相切,
所以
| |t-k| | ||
|
| t2-1 |
| t |
把y=kx+t代入
| x2 |
| 16 |
| y2 |
| 12 |
设M(x1,y1),N(x2,y2),则有x1+x2=-
| 8kt |
| 3+4k2 |
| 6t |
| 3+4k2 |
因为λ
| OC |
所以C(
| -8kt |
| (3+4k2)λ |
| 6t |
| (3+4k2)λ |
又因为点C在椭圆上,
所以
| 4k2t2 |
| (3+4k2)2λ2 |
| 3t2 |
| (3+4k2)2λ2 |
| t2 |
| 3+4k2 |
| 1 | ||||
(
|
因为t2>0,所以 (
| 1 |
| t2 |
| 1 |
| t2 |
所以0<λ2<1,
所以λ的取值范围为(-1,0)∪(0,1).
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查平面向量的运算、直线与圆相切及韦达定理,考查学生综合运用知识分析解决问题的能力,对能力要求高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
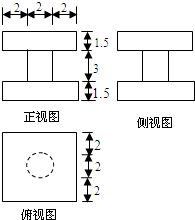 (2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为
(2013•丽水一模)某几何体的三视图如图所示,则该几何体的体积为 (2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),
(2013•丽水一模)已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1),