题目内容
(本题满分16分)本题共3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.
在平面直角坐标系 中,对于直线
中,对于直线 :
: 和点
和点 记
记 若
若 <0,则称点
<0,则称点 被直线
被直线 分隔.若曲线C与直线
分隔.若曲线C与直线 没有公共点,且曲线C上存在点
没有公共点,且曲线C上存在点 被直线
被直线 分隔,则称直线
分隔,则称直线 为曲线C的一条分隔线.
为曲线C的一条分隔线.
⑴求证:点 被直线
被直线 分隔;
分隔;
⑵若直线 是曲线
是曲线 的分隔线,求实数
的分隔线,求实数 的取值范围;
的取值范围;
⑶动点M到点 的距离与到
的距离与到 轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
在平面直角坐标系
 中,对于直线
中,对于直线 :
: 和点
和点 记
记 若
若 <0,则称点
<0,则称点 被直线
被直线 分隔.若曲线C与直线
分隔.若曲线C与直线 没有公共点,且曲线C上存在点
没有公共点,且曲线C上存在点 被直线
被直线 分隔,则称直线
分隔,则称直线 为曲线C的一条分隔线.
为曲线C的一条分隔线.⑴求证:点
 被直线
被直线 分隔;
分隔;⑵若直线
 是曲线
是曲线 的分隔线,求实数
的分隔线,求实数 的取值范围;
的取值范围;⑶动点M到点
 的距离与到
的距离与到 轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.(1)证明见解析;(2)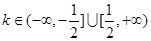 ;(3)证明见解析.
;(3)证明见解析.
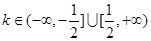 ;(3)证明见解析.
;(3)证明见解析.试题分析:本题属于新定义问题,(1)我们只要利用题设定义求出
 的值,若
的值,若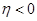 ,则结论就可得证;(2)直线
,则结论就可得证;(2)直线 是曲线
是曲线 的分隔线,首先直线与曲线无交点,即直线方程与曲线方程联立方程组
的分隔线,首先直线与曲线无交点,即直线方程与曲线方程联立方程组 ,方程组应无实解,方程组变形为
,方程组应无实解,方程组变形为 ,此方程就无实解,注意分类讨论,按二次项系数为0和不为0分类,然后在曲线上找到两点位于直线
,此方程就无实解,注意分类讨论,按二次项系数为0和不为0分类,然后在曲线上找到两点位于直线 的两侧.则可得到所求范围;(3)首先求出轨迹
的两侧.则可得到所求范围;(3)首先求出轨迹 的方程
的方程 ,化简为
,化简为 ,过原点的直线中,当斜率存在时设其方程为
,过原点的直线中,当斜率存在时设其方程为 ,然后解方程组
,然后解方程组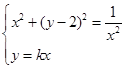 ,变形为
,变形为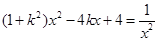 ,这个方程有无实数解,直接判断不方便,可转化为判断函数
,这个方程有无实数解,直接判断不方便,可转化为判断函数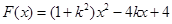 与
与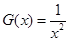 的图象有无交点,而这可利用函数图象直接判断.
的图象有无交点,而这可利用函数图象直接判断.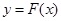 是开口方向向上的二次函数,
是开口方向向上的二次函数,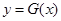 是幂函数,其图象一定有交点,因此直线
是幂函数,其图象一定有交点,因此直线 不是
不是 的分隔线,过原点的直线还有一条就是
的分隔线,过原点的直线还有一条就是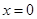 ,它显然与曲线
,它显然与曲线 无交点,又曲线
无交点,又曲线 上两点
上两点 一定在直线
一定在直线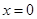 两侧,故它是分隔线,结论得证.
两侧,故它是分隔线,结论得证.试题解析:(1)由题得,
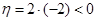 ,∴
,∴ 被直线
被直线 分隔.
分隔.(2)由题得,直线
 与曲线
与曲线 无交点
无交点即
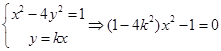 无解
无解∴
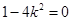 或
或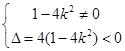 ,∴
,∴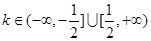 .
.又对任意的
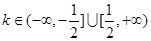 ,点
,点 和
和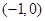 在曲线
在曲线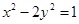 上,满足
上,满足 ,被直线
,被直线 分隔,所以所求
分隔,所以所求 的范围是
的范围是 .
.(3)由题得,设
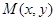 ,∴
,∴ ,
,化简得,点
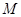 的轨迹方程为
的轨迹方程为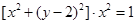
①当过原点的直线斜率存在时,设方程为
 .
.联立方程,
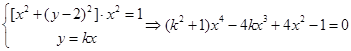 .
.令
 ,因为
,因为 ,
,所以方程
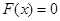 有实解,直线
有实解,直线 与曲线
与曲线 有交点.直线
有交点.直线 不是曲线
不是曲线 的分隔线.
的分隔线.②当过原点的直线斜率不存在时,其方程为
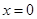 .
.显然
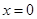 与曲线
与曲线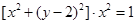 没有交点,又曲线
没有交点,又曲线 上的两点
上的两点 对于直线
对于直线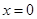 满足
满足 ,即点
,即点 被直线
被直线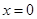 分隔.所以直线
分隔.所以直线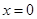 是
是 分隔线.
分隔线.综上所述,仅存在一条直线
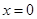 是
是 的分割线.
的分割线.【考点】新定义,直线与曲线的公共点问题.

练习册系列答案
相关题目
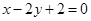 垂直,且在两坐标轴上截距之和为3的直线
垂直,且在两坐标轴上截距之和为3的直线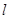 的方程?
的方程? )直线
)直线 过原点,且与线段AB有交点,则直线
过原点,且与线段AB有交点,则直线

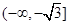

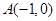 且斜率为
且斜率为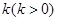 的直线与抛物线
的直线与抛物线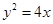 相交于
相交于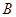 ,
,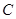 两点,若
两点,若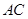 中点,则
中点,则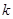 的值是 .
的值是 .