题目内容
已知球O的表面积为12π.
(1)求球O的半径;
(2)已知正方体ABCD-A1B1C1D1的顶点都在球O的球面上,求这个球的体积与正方体ABCD-A1B1C1D1的体积之比.
(1)求球O的半径;
(2)已知正方体ABCD-A1B1C1D1的顶点都在球O的球面上,求这个球的体积与正方体ABCD-A1B1C1D1的体积之比.
分析:(1)先利用球的表面积计算公式,求得球的半径即可;
(2)先求正方体的棱长为a和球的半径为R之间的数量关系,利用体积公式可求出体积之比.
(2)先求正方体的棱长为a和球的半径为R之间的数量关系,利用体积公式可求出体积之比.
解答:解:(1)设球的半径为R,依题意:
球的表面积s=4πR2=12π,解得R=
故球O的半径为
;
(2)设正方体的棱长为a,球的半径为R(其中R=
)
则
a=2R,∴R=
a,
∴正方体ABCD-A1B1C1D1的体积与球O的体积之比为
=
=
,
即这个球的体积与正方体ABCD-A1B1C1D1的体积之比为
π:2.
球的表面积s=4πR2=12π,解得R=
| 3 |
故球O的半径为
| 3 |
(2)设正方体的棱长为a,球的半径为R(其中R=
| 3 |
则
| 3 |
| ||
| 2 |
∴正方体ABCD-A1B1C1D1的体积与球O的体积之比为
| a3 | ||
|
| a3 | ||||||
|
| 2 | ||
|
即这个球的体积与正方体ABCD-A1B1C1D1的体积之比为
| 3 |
点评:本题考查了球的表面积计算公式,考查了正方体和球的体积,也考查了空间想象力,要清楚正方体的体对角线就是圆的直径.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
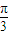 ,则二面角M=OC-B的大小为 .
,则二面角M=OC-B的大小为 .