题目内容
已知球O的表面积为8π,A,B,C是球面上的三点,点M是AB的中点,AB=2,BC=1,∠ABC=
,则二面角M=OC-B的大小为
| π |
| 3 |
arctan
| 6 |
arctan
.| 6 |
分析:首先判断得出△ACB为RT△,从而 OM⊥面QMC,过B作BE⊥MC,再过B作BF⊥OC,连接EF,则∠BFE为面角M-OC-B的平面角.
解答: 解:在三角形ABC中,AB=2,BC=1,∠ABC=
解:在三角形ABC中,AB=2,BC=1,∠ABC=
,由余弦定理,得出AC2=AB2+CB2-2AB•CBcos∠ABC=1+4-2×1×2×
=3,AC=
,AC2+CB2=AB2
∴△ACB为RT△,
∵点M是AB的中点,所以M为△ABC的外心,即为过点A,B,C的截面圆圆心,
由球的截面圆性质可得OM⊥面ABC,过B作BE⊥MC,则OM⊥BE,得出BE⊥面OMC,
∴BE⊥OC,
再过B作BF⊥OC,连接EF,则OC⊥面BFE.
∠BFE为面角M-OC-B的平面角.
易知△BMC为正三角形,BE=
,
S△OBC=
BC×h=
OC×BF而h=
=
=
.
∴BF=
=
.
由勾股定理EF2=BF2-BE2=
∴tan∠BFE=
=
=
.∠BFE=arctan
故答案为:arctan
 解:在三角形ABC中,AB=2,BC=1,∠ABC=
解:在三角形ABC中,AB=2,BC=1,∠ABC=| π |
| 3 |
| 1 |
| 2 |
| 3 |
∴△ACB为RT△,
∵点M是AB的中点,所以M为△ABC的外心,即为过点A,B,C的截面圆圆心,
由球的截面圆性质可得OM⊥面ABC,过B作BE⊥MC,则OM⊥BE,得出BE⊥面OMC,
∴BE⊥OC,
再过B作BF⊥OC,连接EF,则OC⊥面BFE.
∠BFE为面角M-OC-B的平面角.
易知△BMC为正三角形,BE=
| ||
| 2 |
S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
OB2-(
|
2-
|
| ||
| 2 |
∴BF=
1×
| ||||
|
| ||
| 4 |
由勾股定理EF2=BF2-BE2=
| ||
| 4 |
∴tan∠BFE=
| BE |
| EF |
| ||||
|
| 6 |
| 6 |
故答案为:arctan
| 6 |
点评:本题考查二面角大小求解,考查空间想象能力、推理论证、计算、转化能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
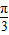 ,则二面角M=OC-B的大小为 .
,则二面角M=OC-B的大小为 .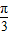 ,则二面角M=OC-B的大小为 .
,则二面角M=OC-B的大小为 .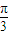 ,则二面角M=OC-B的大小为 .
,则二面角M=OC-B的大小为 .