题目内容
7.过抛物线y2=4x的焦点F作倾斜角为60°的直线,交抛物线于A,B两点(A在x轴上方),那么$\frac{{|{AF}|}}{{|{BF}|}}$=( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 3 | D. | 2 |
分析 设出A、B坐标,利用抛物线焦半径公式求出|AB|,结合抛物线的性质,求出A、B的坐标,然后求比值$\frac{{|{AF}|}}{{|{BF}|}}$即可.
解答 解:设A(x1,y1),B(x2,y2),则抛物线y2=4x中p=2.
|AB|=x1+x2+p=$\frac{2p}{si{m}^{2}θ}$=$\frac{8p}{3}$
∴x1+x2=$\frac{10}{3}$,
又x1x2=$\frac{{p}^{2}}{4}$=1,可得x1=3,x2=$\frac{1}{3}$,
则$\frac{{|{AF}|}}{{|{BF}|}}$=$\frac{3+1}{\frac{1}{3}+1}$=3,
故选:C.
点评 本题主要考察了直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要善于运用抛物线的定义解决问题.

练习册系列答案
相关题目
18.已知函数y=lg(x2-3x+2)的定义域为A,y=lg(x-1)+lg(x-2)的定义域为B,则( )
| A. | A∩B=∅ | B. | A=B | C. | A?B | D. | B?A |
15.方程xy2-x2y=8x所表示的曲线( )
| A. | 关于y轴对称 | B. | 关于y+x=0对称 | C. | 关于原点对称 | D. | 关于x-y=0对称 |
19.设ξ~N(1,σ2),则函数f(x)=x2+2x+ξ不存在零点的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
16.某个几何体的三视图如图所示,则该几何体的体积是( )
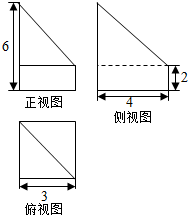

| A. | 30 | B. | 40 | C. | 24 | D. | 72 |