题目内容
已知数列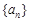 的首项
的首项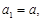 其中
其中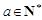 ,
,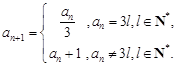 ,令集合
,令集合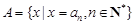 .
.
(1)若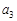 是数列
是数列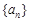 中首次为1的项,请写出所有这样数列的前三项;
中首次为1的项,请写出所有这样数列的前三项;
(2)求证:对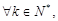 恒有
恒有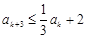 成立;
成立;
(3)求证: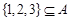 .
.
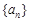 的首项
的首项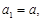 其中
其中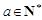 ,
,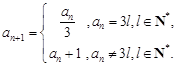 ,令集合
,令集合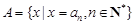 .
.(1)若
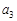 是数列
是数列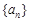 中首次为1的项,请写出所有这样数列的前三项;
中首次为1的项,请写出所有这样数列的前三项;(2)求证:对
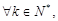 恒有
恒有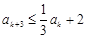 成立;
成立;(3)求证:
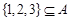 .
.(1)9,3,1或2,3,1;(2)详见解析;(3)详见解析.
试题分析:(1)从
 入手,反过来求
入手,反过来求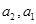 .从条件可看出,首先分
.从条件可看出,首先分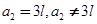 讨论,然后分
讨论,然后分 讨论.
讨论.(2)首先由递推公式将
 用
用 表示出来,再与
表示出来,再与 比较即可.
比较即可.(3)注意
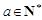 .当
.当 或2、3时,可求出前三项,前三项就是1、2、3三个数,结论成立.
或2、3时,可求出前三项,前三项就是1、2、3三个数,结论成立.那么当
 时,结论是否成立?由递推公式的结构
时,结论是否成立?由递推公式的结构 可以看出,当
可以看出,当 时,数列中的项最终必将小于或等于3.现在的问题是如何来证明这一点.注意(2)小题的结论,由
时,数列中的项最终必将小于或等于3.现在的问题是如何来证明这一点.注意(2)小题的结论,由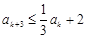 可得
可得 ,这说明,“若
,这说明,“若 ,则
,则 ”,这样依次递减下去,数列中的项最终必将小于或等于3.一旦小于等于3,则必有1、2、3,从而问题得证.
”,这样依次递减下去,数列中的项最终必将小于或等于3.一旦小于等于3,则必有1、2、3,从而问题得证.试题解析:(1)由题设知,数列
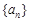 各项均大于0.
各项均大于0.当
 时,
时, .若
.若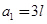 ,则
,则 ;若
;若 ,则
,则 .
.所以前三项分别为9,3,1或2,3,1.
当
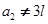 时,
时,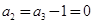 ,不合题意,舍去.
,不合题意,舍去.综上得,前三项分别为9,3,1或2,3,1.
(2)①当
 被3除余1时,由已知可得
被3除余1时,由已知可得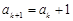 ,
,
 ;
;②当
 被3除余2时,由已知可得
被3除余2时,由已知可得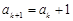 ,
, .
.若
 仍为3的倍数,则
仍为3的倍数,则 ;若
;若 不为3的倍数,则
不为3的倍数,则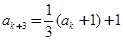 .
.总之,都有

 ;
;③当
 被3除余0时,由已知可得
被3除余0时,由已知可得 .
.若
 都是3的倍数,则
都是3的倍数,则 .
.若
 是3的倍数,
是3的倍数, 不是3的倍数,则
不是3的倍数,则 .
.若
 不是3的倍数,
不是3的倍数, 是3的倍数,则
是3的倍数,则 .
.以上三种情况,都有
 ;
;综合①②③,有
 .
.(3)注意
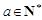 .若
.若 ,则
,则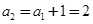 ,
,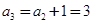 .
.若
 ,则
,则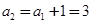 ,
, .
.若
 ,则
,则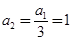 ,
, .
.以上三种情况都有
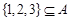 (实际上
(实际上 ).
).下面证明,当
 时,数列
时,数列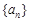 中必存在某一项
中必存在某一项 .
.由(2)可得
 ,
,所以,对于数列
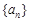 中的任意一项
中的任意一项 ,“若
,“若 ,则
,则 ”.由此可知,若
”.由此可知,若 仍然大于3,则
仍然大于3,则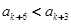 ,这样依次递减下去,最终必存在某一项
,这样依次递减下去,最终必存在某一项 .
.所以如果
 ,则数列
,则数列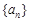 中必存在某一项
中必存在某一项 .
.由前面的计算知,只要数列中存在小于等于3的项,则必有1、2、3三个数,
所以
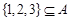 .
.
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
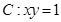 ,过
,过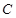 上一点
上一点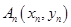 作一斜率为
作一斜率为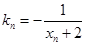 的直线交曲线
的直线交曲线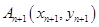 (
(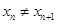 且
且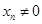 ,点列
,点列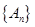 的横坐标构成数列
的横坐标构成数列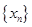 ,其中
,其中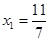 .
.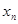 与
与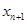 的关系式;
的关系式;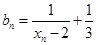 ,求证:数列
,求证:数列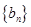 是等比数列;
是等比数列;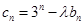 (
(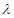 为非零整数,
为非零整数,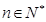 ),试确定
),试确定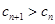 成立.
成立.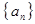 中,
中,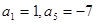 ,
,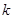 项和
项和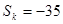 ,求
,求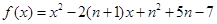 .
.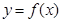 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列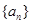 ,求证:
,求证: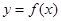 的图像的顶点到
的图像的顶点到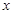 轴的距离构成数列
轴的距离构成数列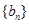 ,求
,求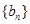 的前
的前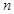 项和
项和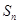 .
. 中,
中, ,
, 则
则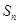 的最大值为____________.
的最大值为____________. ,
, 满足
满足 ,
, , 则数列
, 则数列 的前
的前 项的和为 ( )
项的和为 ( )
 .
.

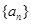 中,公差
中,公差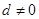 ,且
,且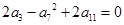 ,数列
,数列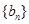 是等比数列,且
是等比数列,且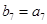 则
则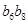 = .
= . 中
中 ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 为
为 的最大值
的最大值
