题目内容
13.曲线y=$\sqrt{1-(x-1)^{2}}$与x轴所围成的区域的面积为( )| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
分析 求出曲线表示上半圆(x-1)2+y2=1,圆心(1,0),半径为1.求出半圆的面积即可.
解答 解:曲线y=$\sqrt{1-(x-1)^{2}}$,
即为上半圆(x-1)2+y2=1,圆心(1,0),半径为1.
曲线y=$\sqrt{1-(x-1)^{2}}$与x轴所围成的区域的面积为${∫}_{0}^{2}$$\sqrt{1-(x-1)^{2}}$dx
=$\frac{1}{2}$π•12=$\frac{π}{2}$.
故选:B.
点评 本题考查定积分的运算,注意运用圆的面积,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.已知一个几何体的三视图如图所示,若该几何体的体积为$\frac{10}{3}$,则a+b2的最小值为( )
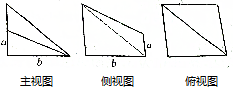

| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
 的单调递增区间是 .
的单调递增区间是 .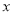 标记.
标记.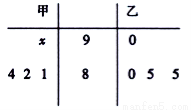
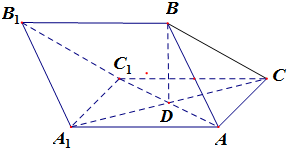 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.