题目内容
已知函数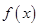 满足如下条件:当
满足如下条件:当 时,
时,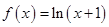 ,且对任
,且对任
意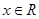 ,都有
,都有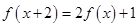 .
.
(1)求函数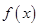 的图象在点
的图象在点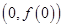 处的切线方程;
处的切线方程;
(2)求当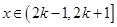 ,
,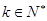 时,函数
时,函数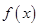 的解析式;
的解析式;
(3)是否存在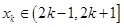 ,
,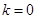 、
、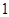 、
、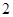 、
、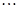 、
、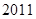 ,使得等式
,使得等式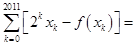
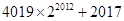 成立?若存在就求出
成立?若存在就求出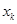 (
(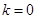 、
、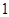 、
、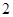 、
、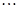 、
、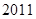 ),若不存在,说明理由.
),若不存在,说明理由.
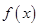 满足如下条件:当
满足如下条件:当 时,
时,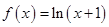 ,且对任
,且对任意
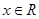 ,都有
,都有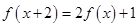 .
.(1)求函数
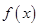 的图象在点
的图象在点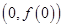 处的切线方程;
处的切线方程;(2)求当
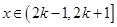 ,
,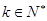 时,函数
时,函数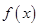 的解析式;
的解析式;(3)是否存在
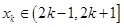 ,
,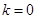 、
、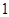 、
、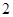 、
、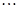 、
、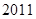 ,使得等式
,使得等式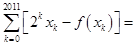
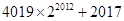 成立?若存在就求出
成立?若存在就求出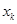 (
(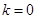 、
、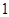 、
、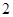 、
、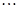 、
、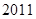 ),若不存在,说明理由.
),若不存在,说明理由.(1)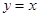 ;(2)
;(2)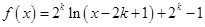 ;(3)详见解析.
;(3)详见解析.
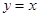 ;(2)
;(2)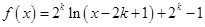 ;(3)详见解析.
;(3)详见解析.试题分析:(1)先求出
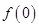 与
与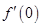 的值,利用点斜式求出相应的切线方程;(2)利用题中的条件结合迭
的值,利用点斜式求出相应的切线方程;(2)利用题中的条件结合迭代法求出函数
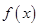 在区间
在区间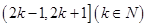 上的解析式;(3)构造新函数
上的解析式;(3)构造新函数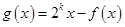 ,考
,考查函数
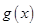 在区间
在区间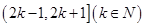 上的单调性,求出函数
上的单调性,求出函数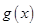 在区间
在区间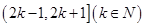 上
上的最小值
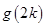 ,于是得到
,于是得到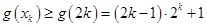 ,然后利用分组求和法与错位相减法来证明
,然后利用分组求和法与错位相减法来证明题中相应的等式.
(1)
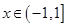 时,
时,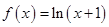 ,
,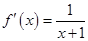 ,
, 所以,函数
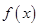 的图象在点
的图象在点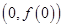 处的切线方程为
处的切线方程为 ,即
,即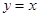 ;
;(2)因为
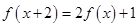 ,
,所以,当
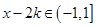 ,
,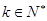 时,
时,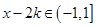 ,
, 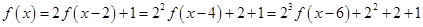
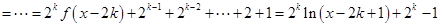 ;
;(3)考虑函数
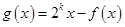 ,
,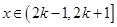 ,
,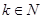 ,
,则
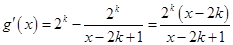 ,
,当
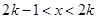 时,
时,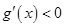 ,
,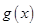 单调递减;
单调递减;当
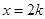 时,
时, ;
;当
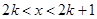 时,
时,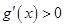 ,
,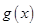 单调递增;
单调递增;所以,当
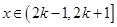 ,
,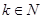 时,
时, ,
,当且仅当
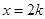 时,
时,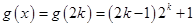 .
.所以,
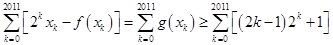 ,
,而
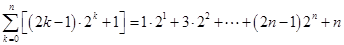 ,
,令
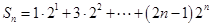 ,则
,则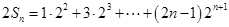 ,
,两式相减得,
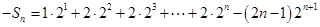
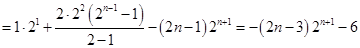 ,
,所以,
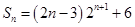 ,
,故
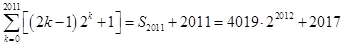 ,
,所以,
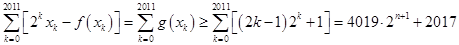 ,
,当且仅当
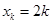 ,
,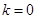 、
、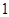 、
、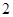 、
、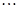 、
、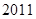 时,
时,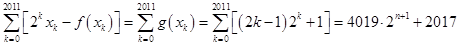 ,
,所以,存在唯一一组实数
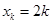 ,
,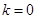 、
、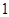 、
、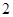 、
、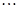 、
、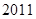 ,
,使得等式
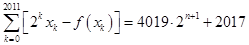 成立.
成立.
练习册系列答案
相关题目
 x3-ax+1.
x3-ax+1.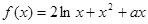 ,若曲线
,若曲线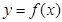 存在与直线
存在与直线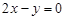 平行的切线,则实数
平行的切线,则实数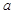 的取值范围是( )
的取值范围是( )



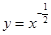 在点
在点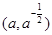 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则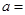 ( )
( ) 在点(1,-
在点(1,- )处切线的倾斜角为( )
)处切线的倾斜角为( )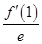 ·ex-f(0)x+
·ex-f(0)x+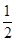 x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________. .
.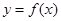 在
在 处的切线与直线
处的切线与直线 平行,求a的值;
平行,求a的值; 时,求
时,求 的单调区间.
的单调区间.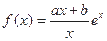 (
(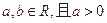 ).
).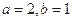 ,求函数
,求函数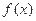 的极值;
的极值;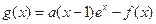 .
.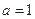 时,对任意
时,对任意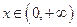 ,都有
,都有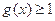 成立,求
成立,求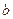 的最大值;
的最大值;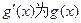 的导函数.若存在
的导函数.若存在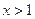 ,使
,使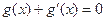 成立,求
成立,求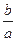 的取值范围.
的取值范围.