题目内容
如图所示，在底面是菱形的四棱锥P-ABCD中，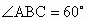
，AP=AC=a，
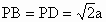，点E在PD上，且PE∶ED=2∶1．
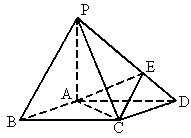
(1)证明：PA⊥平面ABCD；
(2)求以AC为棱，EAC与DAC为面的二面角的大小；
(3)在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论．
答案：略
解析：
解析：
|
(1)证明：略．(2)解：略． (3)解：当F是棱PC的中点时，BF∥平面AEC，如图所示，证明如下． 取PE的中点M，连结FM，则FM∥CE．
由  ，知E是MD的中点．
连结 BM、BD，设BD∩AC=O，则O为BD的中点．∴ BM∥OE．∵ BM∩FM=M，OE∩CE=E，∴平面 BMF∥平面AEC．又  平面BMF，∴BF∥平面AEC． |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
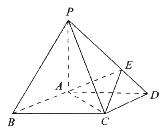
如图所示，在底面是直角梯形的四棱锥P-ABCD中，∠DAB=90°，面PAC⊥平面ABCD，
，AP=AC=a，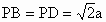
，点E在PD上，且PE∶ED=2∶1．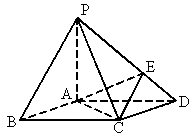
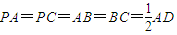，PB=PD=
．点E在PD上，且PE：ED=2：1．
的大小；
，M是PD的中点．
．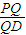