题目内容
 如图所示,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,面PAC⊥平面ABCD,PA=PC=AB=BC=
如图所示,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,面PAC⊥平面ABCD,PA=PC=AB=BC=| 1 |
| 2 |
(1)求证:MC∥平面PAB;
(2)求CM与平面PBC所成角的正弦值;
(3)已知点Q是棱PD上的一点,若二面角Q-AC-D为45°,求
| PQ |
| QD |
分析:过点A作底面ABCD的垂线,由∠DAB=90°,以A为原点建立空间直角坐标系,设PA=2,则B(2,0,0),C(2,2,0),D(0,4,0),P(1,1,
).
(1)由M为PD中点,知M(
,
,
),所以
=(-
,
,
),
=(2,0,0),
=(1,1,
),设
=x
+y
,得到
=-
+
,由此能够证明CM∥平面PAB.
(2)
=(0,2,0),
=(-1,1,
),设平面PBC的法向量为
=(x,y,z),由
,得
=(
,0,1),由此能求出CM与平面PBC所成角的正弦值.
(3)设
=λ,λ∈(0,1),则
=
+λ
=(1-λ,1+3λ,
(1-λ))
=(2,2,0),设平面QAC的法向量为
=(x′,y′,z′),由
,得
=(1,-1,
),
平面ABCD的法向量
=(0,0,1),由二面角Q-AC-D为45°,能求出
=
.
| 2 |
(1)由M为PD中点,知M(
| 1 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
| CM |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| AP |
| 2 |
| CM |
| AB |
| AP |
| CM |
| AB |
| 1 |
| 2 |
| AP |
(2)
| BC |
| BP |
| 2 |
| n |
|
| n |
| 2 |
(3)设
| PQ |
| PD |
| AQ |
| AP |
| PQ |
| 2 |
| AC |
| m |
|
| m |
2
| ||
| 1-λ |
平面ABCD的法向量
| k |
| PQ |
| QD |
| 1 |
| 2 |
解答: 解:过点A作底面ABCD的垂线,
解:过点A作底面ABCD的垂线,
又∵∠DAB=90°
∴可以A为原点建立空间直角坐标系,如图所示
取AC中点H,
∵PA=PB,∴PH⊥AC,
∵面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC
∴PH⊥平面ABCD
不妨设PA=2,则由已知条件可得:B(2,0,0),C(2,2,0),D(0,4,0),P(1,1,
).
(1)证明:∵M为PD中点,
∴M(
,
,
),
∴
=(-
,
,
),
=(2,0,0),
=(1,1,
),
设
=x
+y
,
则
,∴
,
∴
=-
+
,
∴
∥平面PAB,
∵CM?平面PAB,
∴CM∥平面PAB.
(2)
=(0,2,0),
=(-1,1,
),
设平面PBC的法向量为
=(x,y,z),
由
•
=0,
•
=0可得
,
可得一个法向量
=(
,0,1).
设CM与平面PBC所成角为θ,
则sinθ=|cos<
,
>|=
=
.
(3)设
=λ,λ∈(0,1),
则
=
+λ
=(1-λ,1+3λ,
(1-λ))
=(2,2,0),
设平面QAC的法向量为
=(x′,y′,z′),
由
•
=0,
•
=0得
,
可得一个法向量
=(1,-1,
),
平面ABCD的法向量
=(0,0,1),
由二面角Q-AC-D为45°可得
=|cos<
,
>|,
即
=
,
解得λ=
,或λ=-1(舍).
所以
=
,
所以
=
.
 解:过点A作底面ABCD的垂线,
解:过点A作底面ABCD的垂线,又∵∠DAB=90°
∴可以A为原点建立空间直角坐标系,如图所示
取AC中点H,
∵PA=PB,∴PH⊥AC,
∵面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC
∴PH⊥平面ABCD
不妨设PA=2,则由已知条件可得:B(2,0,0),C(2,2,0),D(0,4,0),P(1,1,
| 2 |
(1)证明:∵M为PD中点,
∴M(
| 1 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
∴
| CM |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| AB |
| AP |
| 2 |
设
| CM |
| AB |
| AP |
则
|
|
∴
| CM |
| AB |
| 1 |
| 2 |
| AP |
∴
| CM |
∵CM?平面PAB,
∴CM∥平面PAB.
(2)
| BC |
| BP |
| 2 |
设平面PBC的法向量为
| n |
由
| BC |
| n |
| BP |
| n |
|
可得一个法向量
| n |
| 2 |
设CM与平面PBC所成角为θ,
则sinθ=|cos<
| CM |
| n |
| ||||
|
|
| ||
| 3 |
(3)设
| PQ |
| PD |
则
| AQ |
| AP |
| PQ |
| 2 |
| AC |
设平面QAC的法向量为
| m |
由
| AC |
| m |
| AQ |
| m |
|
可得一个法向量
| m |
2
| ||
| 1-λ |
平面ABCD的法向量
| k |
由二面角Q-AC-D为45°可得
| ||
| 2 |
| m |
| k |
即
| ||
2+
|
| 1 |
| 2 |
解得λ=
| 1 |
| 3 |
所以
| PQ |
| PD |
| 1 |
| 3 |
所以
| PQ |
| QD |
| 1 |
| 2 |
点评:本题考查直线与平面平行的证明,直线与平南所成角的正弦值的求法和二面角的应用,考查考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,是高考的重点.解题时要认真审题,注意向量法的灵活运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
 ,BC=CC1=1,P是BC1上一动点,则
,BC=CC1=1,P是BC1上一动点,则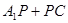 的最小值是_____.
的最小值是_____.


 ,BC=CC1=1,P是BC1上一动点,则
,BC=CC1=1,P是BC1上一动点,则 的最小值是_____.
的最小值是_____.