题目内容

函数y=sin(-x+
π
4
)的单调递减区间是
 
．
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：由复合函数的单调性只需求y=sin（x-
π
4
）的单调递增区间即可，解不等式2kπ-
π
2
≤x-
π
4
≤2kπ+
π
2
可得答案．
解答： 解：变形可得y=sin(-x+
π
4
)=-sin（x-
π
4
），
由复合函数的单调性只需求y=sin（x-
π
4
）的单调递增区间即可，
由2kπ-
π
2
≤x-
π
4
≤2kπ+
π
2
可得2kπ-
π
4
≤x≤2kπ+
3π
4
，
∴所求单调区间为[2kπ-
π
4
，2kπ+
3π
4
]（k∈Z）
故答案为：[2kπ-
π
4
，2kπ+
3π
4
]（k∈Z）
点评：本题考查三角函数的单调性，涉及复合函数的单调性，属基础题．
练习册系列答案
相关题目
已知一个三棱柱的三视图如图所示，则该三棱柱的表面积为（　　）
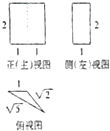
A、4
5
+4
2
+5
B、2
5
+2
2
+
5
2
C、
2
5
+2
2
+3
3
D、2
5
+2
2
+3
已知平面α，β，直线l，m，且有l⊥α，m?β，给出下列命题：
①若α∥β则l⊥m；
②若l∥m则l∥β；
③若α⊥β则l∥m；
④若l⊥m则l⊥β；
其中，正确命题有
 
．（将正确的序号都填上）
垂直于同一条直线的两条直线的位置关系是
 
．
已知函数f（x）=sin2ωx+
3
sinωxsin（ωx+
π
2
）（ω＞0）的最小正周期为
π
2
．
（1）写出函数f（x）的单调递增区间；
（2）求函数f（x）在区间[0，
π
3
]上的取值范围．
定义在R上的偶函数f（x）满足f（x）=f（x+2），当x∈[3，4]时，f（x）=x-2，则有下面三个式子：①f（sin
1
2
）＜f（cos
1
2
）；②f（sin
π
3
）＜f（cos
π
3
）；③f（sin1）＜f（cos1）；其中一定成立的是_____．
若cos（α-
π
6
）=
5
3
，α∈（
π
6
，
π
2
），则sinα=
 
．
求下列不等式（组）的解集，并用区间表示：
（1）3x+4＜5x-6；
（2）
x+3＜4
x+1≥-3
．
已知两直线l1：2x-y+3=0，l2：mx+2y+n=0平行，则m的值是（　　）
A、-4B、-1C、1D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网