题目内容
设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠∅?若存在,请求出a的值;若不存在,说明理由.
假设A∩B≠∅,则方程组
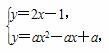 有正整数解,消去y得,
有正整数解,消去y得,
ax2-(a+2)x+a+1=0.(*)
由Δ≥0,有(a+2)2-4a(a+1)≥0,
解得-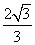 ≤a≤
≤a≤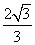 .
.
因a为非零整数,∴a=±1,
当a=-1时,代入(*),解得x=0或x=-1,
而x∈N*.故a≠-1.
当a=1时,代入(*),解得x=1或x=2,符合题意.
故存在a=1,使得A∩B≠∅,
此时A∩B={(1,1),(2,3)}.

考纲要求
1.集合的含义与表示
(1)了解集合的含义、

练习册系列答案
相关题目
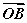 |·
|·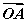 +|
+|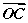 =
= ,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________.
,将它类比到空间情形应该是:若O是四面体ABCD内一点,则有________. 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线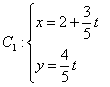 (
(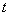 为参数)和曲线
为参数)和曲线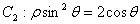 相交于
相交于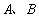 两点,设线段
两点,设线段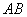 的中点为
的中点为 ,则点
,则点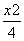 +
+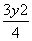 =1},B={y|y=x2},则A∩B=( )
=1},B={y|y=x2},则A∩B=( )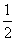 <2x<2},B={x|lgx>-1},则A∪B=( )
<2x<2},B={x|lgx>-1},则A∪B=( )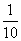 } D.{x|-1<x<10或x>10}
} D.{x|-1<x<10或x>10}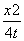 +
+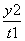 =1表示曲线C,给出以下命题:
=1表示曲线C,给出以下命题: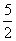 .
.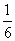 ,-
,-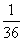 )
)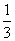 ,-
,-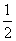 )或(-
)或(-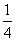 ,
, )
)