题目内容
已知单调递增的等比数列{an}满足a1+a2+a3=14,且a2+1是a1,a3的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an,求数列{bn}的前n项和Sn;
(3)若存在n∈N*,使得Sn+1-2≤8n3λ成立,求实数λ的最小值.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an,求数列{bn}的前n项和Sn;
(3)若存在n∈N*,使得Sn+1-2≤8n3λ成立,求实数λ的最小值.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)将已知条件a1+a2+a3=14,且a1+1是a1,a3的等差中项,用基本量表示,列出方程组,求出首项与公比,利用等比数列的通项公式求出数列{an}的通项.
(2)由bn=anlog2an=n•2n,利用错位相减法能求出数列{bn}的前n项和Sn.
(3)原问题等价于:存在n∈N*,使得λ≥
=
成立,令f(n)=
,只需λ≥f(n)min即可,由此能求出λ的最小值.
(2)由bn=anlog2an=n•2n,利用错位相减法能求出数列{bn}的前n项和Sn.
(3)原问题等价于:存在n∈N*,使得λ≥
| n•2n+1 |
| 8n3 |
| 2n-1 |
| n2 |
| 2n-1 |
| n2 |
解答:
解:(1)设等比数列{an}的公比为q,
∵a1+a2+a3=14,且a2+1是a1,a3的等差中项,
∴
,
解得q=2,a1=2,或q=
,a1=8(舍)
∴an=2n.
(2)bn=anlog2an=n•2n,
∴Sn=1×2+2×22+3×23+…+n×2n,①
2Sn=1×22+2×23+3×24+…+n×2n+1,②
①-②,得-Sn=2+2 2+23+…+2n-n•2n+1
=
-n•2n+1,
∴Sn=(n-1)•2n+1+2.
(3)由(2)知Sn+1=n•2n+2+2,
原问题等价于:存在n∈N*,使得λ≥
=
成立,
令f(n)=
,只需λ≥f(n)min即可,
∵f(n+1)-f(n)=
-
=
,
∴f(n+1)-f(n)的正负取决于n2-2n-1=(n-1)2-2的正负,
∴f(1)>f(2)>f(3),f(3)<f(4)<…
∴f(n)min=f(3)=
,即λ≥
,
∴λ的最小值是
.
∵a1+a2+a3=14,且a2+1是a1,a3的等差中项,
∴
|
解得q=2,a1=2,或q=
| 1 |
| 2 |
∴an=2n.
(2)bn=anlog2an=n•2n,
∴Sn=1×2+2×22+3×23+…+n×2n,①
2Sn=1×22+2×23+3×24+…+n×2n+1,②
①-②,得-Sn=2+2 2+23+…+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
∴Sn=(n-1)•2n+1+2.
(3)由(2)知Sn+1=n•2n+2+2,
原问题等价于:存在n∈N*,使得λ≥
| n•2n+1 |
| 8n3 |
| 2n-1 |
| n2 |
令f(n)=
| 2n-1 |
| n2 |
∵f(n+1)-f(n)=
| 2n |
| (n+1)2 |
| 2n-1 |
| n2 |
| 2n-1(n2-2n-1) |
| n2(n+1)2 |
∴f(n+1)-f(n)的正负取决于n2-2n-1=(n-1)2-2的正负,
∴f(1)>f(2)>f(3),f(3)<f(4)<…
∴f(n)min=f(3)=
| 4 |
| 9 |
| 4 |
| 9 |
∴λ的最小值是
| 4 |
| 9 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查实数的最小值的求法,解题时要注意错位相减法的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
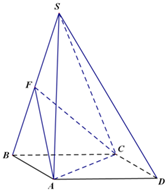 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2